布劳赫方程在非线性光学与光子学中的重要性

设入射光场为沿z轴方向传播并按x轴方向偏振的单色平面波，它在这里可写为

设共振吸收介质为两能级体系，描述该体系的密度矩阵算符ρ满足如下的运动方程：

式中，H=H0+H'，H0是介质无微扰哈密顿量，H'=-p·E（z，t）是相互作用微扰哈密顿量，而p为分子电偶极矩算符。对二能级系统而言，从上述方程出发可导出密度矩阵算符矩阵元满足的方程为［76］

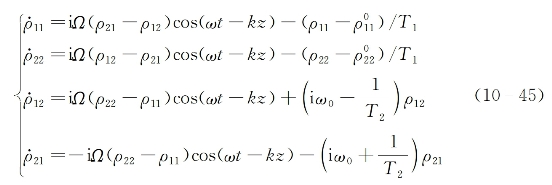
式中，ω0为介质共振跃迁中心频率，Ω为由式（10-35）定义的拉比频率，和为无施加外场时低能级1上和高能级2上的热平衡粒子数分布，T1和T2为唯象引入的弛豫因子，其中，T1在形式上表示与对角矩阵元有关的弛豫衰减时间，而T2则表示与非对角矩阵元有关的弛豫衰减时间。在物理上，T1和T2仍然保留本章前面所给出的定义。

为消除方程组式（10-45）中随光频变化的时间因子，可进一步作如下变换：

这一变换的物理含义，与通过式（10-31）所作坐标变换（x-y-z）→（x'-y'-z）在实质上是等同的，亦即在一个相对于z轴而言光场矢量E不随时间以光频振荡的“静止”坐标系中考查有关物理量之行为。经过这样一种变换，并在忽略非共振高频（如2ωt）项贡献的近似下，式（10-45）变成

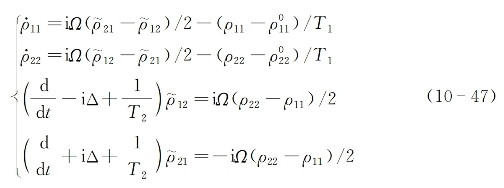
式中，Δ为入射光场频率ω与介质吸收跃迁中心频率ω0的失共振程度。对气体介质来说，

式中，υz是气体分子沿z轴方向的热运动速度分量。基于式（10-47），将同合并以及同合并后可得

在此基础上，再引入一组新的变量：

则式（10-49）可进一步简化为如下的方程，称为光学中的布劳赫方程：

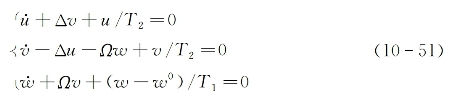
式中，w0=代表无入射光场时两能级间的粒子数密度差。(www.xing528.com)

若所考虑的时间范围远小于T1和T2，则在式（10-51）中可令T1，T2→∞，从而可得到更为简化的布劳赫方程的矢量表示式：

矢量B称为布劳赫矢量，它与另一矢量β在变换后的（x'-y'-z）直角坐标系中的分量表示式为

式中，，，z0为直角坐标系（x'-y'-z）三个轴方向上的单位矢量。引入的位于x'-z平面内的矢量β可称为赝光场矢量，它在x'轴方向上的分量为Ω=（2πp0/h）E0，表征入射光场之强弱，而在z轴方向上的分量为-Δ=ω-ω0-kυz，表征入射光场与粒子体系的失共振程度。这里引入的布劳赫矢量B，可称为描述介质对入射光场反应行为的赝电极化矢量：它在z轴方向上的分量为w=ρ22-ρ11，表征两能级粒子数密度之差；而在x'轴与y'轴方向上的分量分别为u与υ，它们的组合决定了介质的宏观电极化和辐射相干次波的行为。将式（10-52）与式（10-32）相比，可看出两者是一致的，只不过前者是后者求和的结果。

如图10-12（a）所示，式（10-52）表示了布劳赫矢量B绕矢量β的一种进动，该进动频率等于|β|，亦即

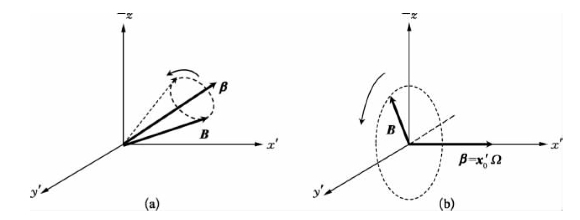
图10-12　布劳赫矢量B围绕位于（x'-z）平面内矢量β的进动

（a）偏离共振情况；（b）准确共振情况

在最简单的可暂时忽略T1和T2弛豫影响的近似条件下，可在式（10-51）中令T1，T2→∞而得到简化的布劳赫方程：

设在t=0时刻光场施加于样品介质中，则在0＜t＜＜T1，T2的时间范围内，式（10-55）具有以下的解：

式中，表征在t=0时刻介质的初始粒子数之差。这组方程解满足的初始条件为

而在这之后任意时刻该矢量的模量保持不变，亦即

在准确共振的条件下，有Δ=0，β=Ω，和u（t）=0。这意味着此情况下矢量β沿x'轴取向，而矢量B则在y'-z平面内以拉比频率Ω绕x'轴旋转，如图10-12（b）所示。对矢量B（t）而言，它在z轴上的投影w（t）决定介质两能级上粒子数之差随时间的变化，而在y'轴上的投影υ（t）则决定介质在光场作用下，具有产生相干次波辐射能力的宏观电简化强度随时间的变化。如果入射相干光场足够强，拉比频率Ω值足够高，则在Ω-1＜t＜＜T1，T2的时间范围内，矢量B（t）可绕x'轴旋转多个回合，这意味着相干次波辐射可多次周期性达到极大。如果在所考虑的时间范围内，T1和T2的弛豫影响不能忽略，矢量B（t）的模量随时间逐渐减小，则可预期出自共振介质的相干次波辐射出现有阻尼的周期性振荡，这就是光学章动效应的基本物理解释。