光子回波的理论描述-来自《非线性光学与光子学》的成果

设所考虑的共振介质仍为由具有二能级结构的粒子（原子或分子）体系所组成，而不同粒子间的快速失相位弛豫，主要是由谱线的非均匀加宽机制所决定。以角标j表示具有相同共振吸收频率值ω0j的一群原子，而不同群原子共振吸收频率值彼此略有差异。在这种情况下，粒子体系的哈密顿量为［29～31］

式中，σx，σy，σz为泡利自旋算符3个矩阵元（被2除），p0为单个粒子共振跃迁电偶极矩算符的矩阵元，Ex，Ey为沿z轴传播的光波电场强度的两个横向分量。

为便于有一个比较直观的描述图像，在这里有必要引入原子体系赝电极化算符：

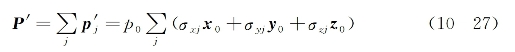
式中，为第j群粒子的赝电偶极矩矢量算符，x0，y0，z0为沿x、y、z轴方向上的单位矢量。假设入射光场是频率为ω并沿z轴方向传播的单色圆偏振光，即

E=Exx0+Eyy0=E0（z，t）［cos（ωt-kz）·x0+sin（ωt-kz）·y0］

式中，E0（z，t）为光场的慢变化振幅函数。同样为数学处理上的方便，与式（10-27）相对应，进一步引入赝电场强度矢量，对第j群原子来说它可具体写为

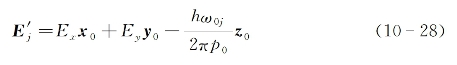
则基于式（10-27）和式（10-28），可将式（10-26）改写为如下简单形式：

矢量P'的期望值可通过系统的密度矩阵算符ρ表示为

这里密度矩阵算符ρ的定义和物理含义可参见18.1节的说明。ρ随时间的变化满足方程：

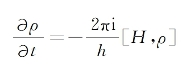
由此可进一步导出第j群原子赝电偶极矩矢量算符期望值随时间的变化为

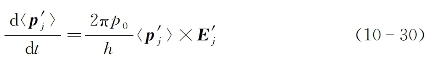
上式的力学图像，相当于描述一个在以光频ω绕z轴旋转的直角坐标系中，矢量围绕矢量的进动。为使图像更加直观和明了，可在一个对于z轴而言是“静止”不动的新坐标系（x'-y'-z）中考查的进动行为，这相当于对系统密度矩阵作如下表象变换：

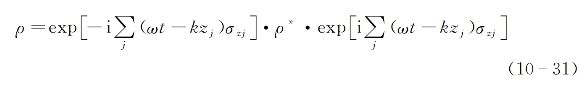
则在新的表象坐标中（所有有关的量在右上角加*号）有如下运动方程成立：

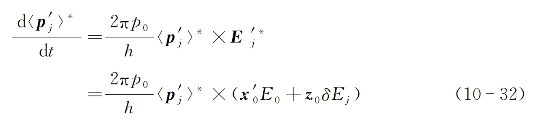
式中，E0为光场振幅函数，而

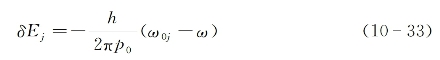
式（10-32）描述的是在新坐标系中，矢量围绕矢量的进动，进动的角频率为

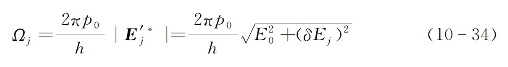
由于在这里考虑的是共振作用，有ω0j-ω≈0和δEj＜＜E0成立，因此进动角频率对所有不同群原子近似相同并可简单表示为

这就是所谓的拉比（Rabi）频率，它决定于原子电偶极跃迁矩阵元p0和入射光场振幅E0的乘积。(www.xing528.com)

在上述新坐标表象中，介质赝电极化矢量可表示为

而与的关系为［30］

在新坐标系中矢量的含义可说明如下：这些矢量在z轴方向上的投影之和表征粒子数在能级上的分布；它们在y'轴方向上投影之和，则代表这些原子对宏观电极化矢量的贡献。在这种理解的基础上，可对光子回波的产生过程作进一步图像式的说明。应该注意的是，介质电极化强度矢量总是决定于众多矢量之和，因此不同矢量之间的相位关系是至关重要的。

如图10-6所示的新坐标系中，只画出了具有相同共振吸收频率（ω0j）的一群原子矢量的取向随时间和入射脉冲作用而变化的行为，可以想象众多对应不同j标记的其他群粒子矢量的相似行为。其中图10-6（a）为光脉冲入射前所有的矢量均沿-z方向取向，代表所有原子均处于低能级，无宏观电极化。图10-6（b）对应于第一个π/2脉冲入射时情况，上下能级粒子数变成相同，所有的矢量旋转90°变成沿y'轴取向，并对介质宏观电极化产生瞬时最大贡献；这是因为按式（10-35），不同原子群对应的绕矢量（即x'0E0，因为δEj＜＜E0）旋转的角度相同并且均为

式中，τ1为第一个脉冲的宽度。在这一时刻，所有不同群原子同步作用（亦即所有矢量指向相同）的结果，是使介质产生最大宏观感应电极化并沿入射光方向发射相干次波辐射，虽然该次波辐射无法与入射脉冲区别开来。图10-6（c）为第一个脉冲通过介质之后的情况，此时有E0→0，但按照式（10-32）和式（10-34），所有不同的矢量仍将在x'-y'平面上继续绕着矢量z0δEj进动，它们的旋转角频率有所不同，并由下式决定：

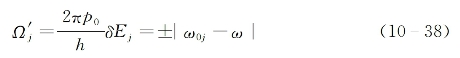
图10-6　在坐标系（x'-y'-z）中光子回波产生的图像式说明

（a）光场入射前；（b）第一个π/2脉冲入射；（c）第一个脉冲通过后失相位过程开始；
（d）第二个π脉冲入射时失相位过程逆转；（e）第二个脉冲通过后τs时刻产生光子回波

这些矢量以不同角频率绕z轴的进动行为，在物理上意味着由非均匀加宽机制造成的激发态原子的快速失相位过程，该过程导致介质宏观感应电极化矢量和由它产生的相干次波辐射随时间快速衰减。为进一步分析这种衰减过程，可单独考虑图10-6（c）中任意一组j原子的行为。对应着式（10-38）中的±符号，可将该群粒子进一步区分为两组：一组原子具有负δEj值而它们的矢量按顺时针方向旋转（s组）；另一组原子具有正δEj值而它们的相应矢量按逆时针方向旋转（f组）。这种区分方法对其他j群粒子也适用，只是不同群粒子对应的相应两组矢量的旋转速度有所不同而已。在经过一段时间间隔τs之后，对每一指定群粒子而言的两组矢量的旋转角度为

如果在这时有第二个π脉冲入射，如图10-6（d）所示的情况，不同原子群对应的和均绕矢量旋转了相同角度：

式中，τ2为第二个脉冲的宽度。在第二个脉冲通过介质后，不同原子群对应的和继续绕z轴向趋近于-y'方向旋转。但在经过τs的时间间隔后，如图10-6（e）所示，所有不同群原子的上述两组矢量分量又同时重合并沿-y'轴方向取向，在物理上意味着复原同相位过程正好全部完成，此时介质宏观电极化强度重新恢复为极大，并发射出相干光频次波辐射——光子回波。

光子回波可认为是由一群具有相同位相关系的大量感应电偶极矩体系相干发射的结果，考虑到介质与光作用区域远远大于光波波长，因此大量电偶极子相干辐射的结果可使回波辐射具有很高的定向性。理论上可以计算出回波的光强为［29］

式中，δV是两入射脉冲在介质样品中的重合作用区域体积，N0为介质的原子密度，I0相当于一个激发态原子对回波光强的贡献，ke为回波波矢，k1，k2分别为第一、第二个激励脉冲的波矢，平均则是按介质与光相互作用区域内不同位置上的原子进行的。由式（10-40）可看出，光子回波光强最大值将发生在满足如下波矢匹配条件的特定方向上：

为使上述条件满足，当k1和k2同方向时，ke也应与它们同向；当k1和k2成微小角度φ0交叉入射时，则ke与k2间夹角也应为φ0。利用光子回波产生的这种波矢匹配条件，便于将回波脉冲与入射激励脉冲在空间上分离开来，从而易于进行检测。

实际上，经常需要测量的是光子回波的信号强度作为两入射激励脉冲间隔（τs）的函数，它并可表为［32］：

基于上面这种关系，研究者们可通过测量回波的信号强度对τs的依赖性而间接确定被测样品的T2值。进一步的分析表明，共振吸收样品的横向弛豫时间T2可表示为［33～35］

式中，T1为纵向弛豫时间（激发态寿命），而在这里则代表介质激发态粒子由各种均匀加宽机制导致的失相位速率。基于上述关系，可以在已知T1大小和测出T2数值后，进一步求出样品介质的值。