非线性光学：2π脉冲形状与速度

下面进一步来求2π脉冲的形状和它在介质中的传播速度。为此，首先将式（10-9）中第二式代入式（10-8）中第一个场方程，可得到描述脉冲传播的方程式为

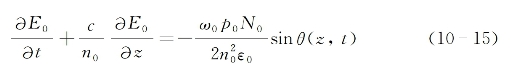
作参量代换，令τ=t-（z/ξ），并注意到

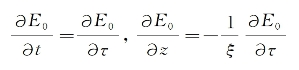
式中，ξ代表脉冲在共振介质中的传播速度，则可以将式（10-15）改写成

式中，

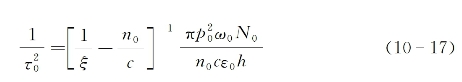
从式（10-16）出发不难推出以下关系成立：

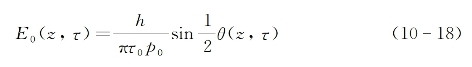
基于式（10-16）和式（10-18），可最后得出一个描述2π脉冲在共振介质中传播时的稳定特解为（参见附录8）［2］

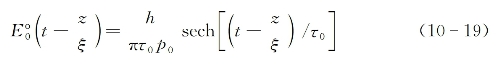
式中，τ0由式（10-17）所决定，它代表稳定2π脉冲的时间宽度。将式（10-19）按变量τ进行积分可得

这一结果证明了由式（10-19）给出的双曲正割函数，的确是稳定2π脉冲的一种适当描述。

从式（10-17）出发可写出2π脉冲在共振介质中的传播速度满足：

式中，α为介质的线性吸收系数并可表示为

(www.xing528.com)

在写出上式过程中假设了跃迁光谱线宽主要由均匀加宽介质所决定。从式（10-21）中可以看出，2π脉冲在共振介质中的传播速度ξ总是小于相速度c/n0；计算表明，对某些共振吸收介质而言，ξ可比c/n0慢102～103量级。

2π脉冲在共振介质中的传播速度变慢的物理原因是，脉冲前半部的作用是通过它自身的吸收把低能级粒子全部泵浦到高能级，而脉冲后半部的作用是通过感应受激发射迫使粒子全部回到低能级并重新释放它们所吸收的能量。这两个作用导致的总结果，是2π脉冲在共振介质传播过程中能量保持不变，而脉冲能量（或波形）传播速度则变慢。

以上考虑都是准确的2π脉冲的性质。为了考查初始值θ（z=0）=θ0为任意的光脉冲在介质内的传播规律，可将θ（z）随在介质内传播距离z的变化表示为［1，2］

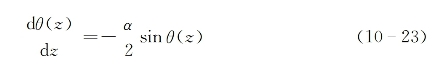
这一方程的通解为

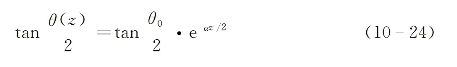
作为一种例子，图10-1给出了具有两种不同脉冲初始值（θ0=0.9π和1.1π）条件下，脉冲面积和形状随在介质内传播距离变化的理论曲线，这里入射脉冲任意假设具有高斯时间波形。

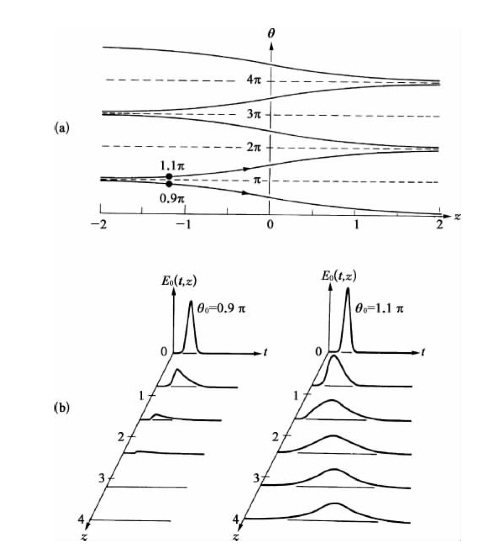
图10-1　具有两给定初始θ0值的脉冲在共振吸收介质的传播［1］

（a）脉冲面积θ（z）沿传播距离z的变化，z=0点为任意选定；（b）脉冲形状沿传播距离z的变化，沿z轴的单位是πα-1（cm）

从图10-1可以看出，当θ0＜π时，入射脉冲很快衰减并在超过几个（πα-1）的距离处衰减为零；但当π＜θ0＜2π时，脉冲面积随传播距离z而增加，直到成为一个稳定的2π脉冲为止。在更一般的情况下，当入射短脉冲具有如下任意初始值：

脉冲在共振吸收介质传播过程中将逐渐分裂，并在经过大于几个（πα-1）的距离处，形成m个稳定的2π脉冲。

到目前为止，考虑的是共振吸收介质，亦即初始时全部粒子处于低能级。如果考虑的是共振增益介质，亦即初始时全部粒子均处于高能级，N（t=0）=-N0，则入射相干短脉冲在该介质中的传播，应遵循以下的规律［3，4］：

（1）仍然存在着稳定的2π脉冲，其能量和形状在传播过程中保持不变。

（2）对于初始面积θ0≥m2π的入射脉冲，在增益介质传播过程中可分裂为m个稳定的2π脉冲。

（3）2π脉冲在共振增益介质中的传播速度，可明显大于光的相速（c/n0）。

形成上述最后一个行为的物理解释是，2π脉冲的前半部的作用是通过迫使介质全部粒子从高能级回到低能级而本身获得能量增益，而脉冲后半部的作用是通过泵浦全部粒子从低能级重新回到高能级而本身能量被吸收。这两个作用的总效果，是使得2π脉冲能量（或波形）传播速度在增益介质中变快。