非线性光学与光子学中的2PA半经典理论

本小节将从半经典理论框架下的三阶电极化理论出发，对2PA基本过程作一简明定量描述。考虑频率分别为ω1和ω2的两束单色激光同时重合入射到某一双光子吸收共振介质，根据式（5-25）～式（5-29），由双光束耦合作用造成的复数折射率变化为

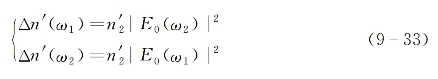
式中，E0（ω1）和E0（ω2）为光场振幅函数，而复数非线性折射率为

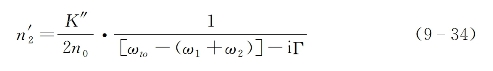
式中，Γ为介质分子2PA跃迁的线宽因子，ωto为该跃迁的中心频率，K"为一个只与介质有关的系数［参见式（5-27）］：

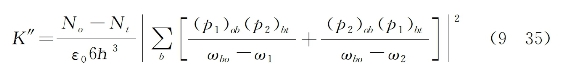
这里No和Nt为如图9-9所示2PA跃迁的低和高能级上分子数密度，p1和p2为分子偶极矩算符在两光束各自偏振方向上的投影，而求和则是按所有可能的分子激发能级b进行。

对于频率为ω1的光束而言，它经受的复折射率变化为

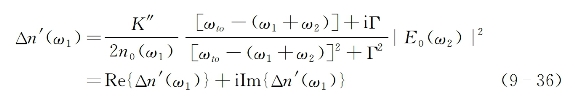
式中，折射率变化量的实部与虚部分别为

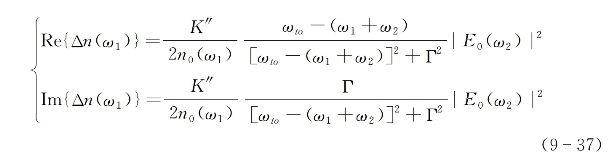
该光束沿z轴方向传输过程中的振幅函数变化为

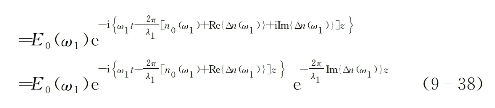
式中，λ1为与频率ω1对应的光束在真空中的波长。在此基础上进一步有

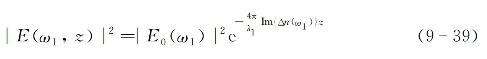
因I（ω1，z）∝|E（ω1，z）|2，故该光束在2PA介质中的光强衰减可写为

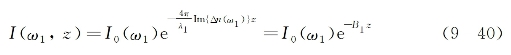
式中，B1为光强指数衰减系数（量纲为cm-1）：

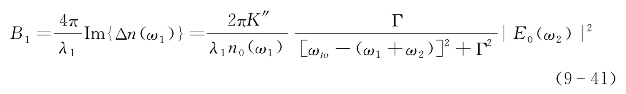
再利用光强与场振幅的关系式［参见式（1-31）］：

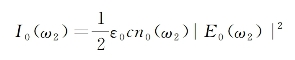(www.xing528.com)

并将式（9-35）代入式（9-41）后可得

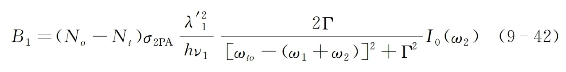
式中，为第一个光束在介质中的波长，σ2PA为单个分子的双光子吸收微分截面（量纲为cm2），其大小为

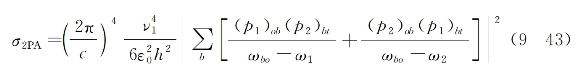
将式（9-43）与式（7-45）相比，可看出两者在形式上很相似。

对于气体样品，通常有B1z＜＜1，则光强衰减式（9-40）可简化为

而光强的相对变化作为（ω1+ω2）的函数可表示为

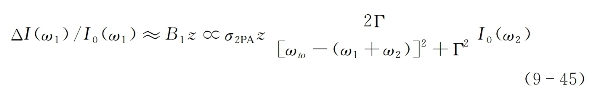
经过相同的推导过程，对另外一束频率为ω2的光束同样有

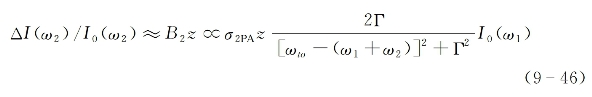
从以上两式可看出，如果不考虑多普勒效应和其他加宽机制，则双光子吸收导致每一光束衰减的共振调谐曲线呈洛伦兹分布线型，自然线宽半峰全宽为2Γ。

在气体样品中考虑到多普勒效应后，单个分子从两束光中同时各吸收一个光子而产生双光子吸收跃迁的概率，可表示为

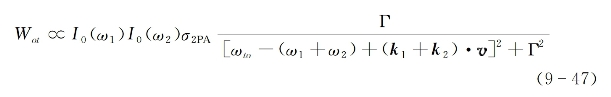
式中，k1和k2为两束光的波矢，υ是该分子的平动速度矢量。如果这两束光反向而行且频率相近，亦即有k1≈-k2，则上式变为

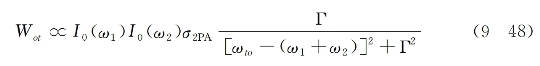
这意味着对所有具有不同运动方向和速度值的气体分子而言，它们由两对撞光束中同时各吸收一个光子的共振行为完全相同，故多普勒效应影响可自动消除。此情况下每一个光束的衰减，仍由式（9-45）或式（9-46）所表示。

在某些实验条件下，为避免每一光束本身双光子吸收（它不能消除多普勒效应的影响）发生的可能，可选择两光束的频率满足（ω1+ω2）=ωto和2ω1≠2ω2≠ωto。

在电偶极近似下的双光子吸收跃迁的选择定则是，跃迁的起始和终止能级的宇称必须相同。特别是当双光子吸收跃迁发生在气体原子的两个S态能级时，跃迁前后原子的角动量应保持不变；此情况下即使两对撞光束具有相同频率但却有相反的圆偏振态，只有来自双光束的2PA能够发生，而来自单光束的2PA被禁止［1，2］。这是消除单光束2PA背底影响的有效方法之一。

就消多普勒效应双光子吸收光谱技术而言，两反向光束可做到准确平行，故角度加宽影响可忽略。通过使用宽光束或者令定向原子束沿光束轴向飞行的措施，可减小渡越加宽的影响。然而，碰撞加宽、反冲加宽以及二次多普勒加宽等影响依然存在。