从如图8-23所示物理模型出发,在数学处理过程中,无论是总的入射泵浦光场,还是总的后向受激散射出射光场,都不需要分解为众多项的级数展开,而只需要分别分解为两部分之和,从而使较为严密的数学求解易于实现。为此,作者等人分别就泵浦光非聚焦入射以及聚焦入射两种情况,从数学上证明了式(8-31)的成立,并同时指出了为此需要满足的具体物理条件[58,69]。为简明起见,下面仅以泵浦光非聚焦入射情况为例,说明该种理论推导的要点[69]。
假设一平面泵浦光束经过一个畸变作用不很大的像差板,然后以准平行光束方式直接入射到散射介质中;此外,只考虑稳态作用情况,亦即光场振幅和波面不随时间而变。
按照前面所采用的物理解释模型并参照图8-23,可将经过像差板后的总的入射泵浦光场表示为两部分之和(不考虑场的偏振特性),即
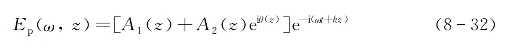
这里假设入射场沿-z轴方向传播,A1(z)和A2(z)分别为总光场中所含平面波和像差波的实振幅函数,θ(z)为像差波的相位因子,它表征该像差波偏离理想波面的程度并且是空间坐标z的函数。
同样,沿+z轴方向传播的总的后向受激散射光场也可表示为两部分之和,即
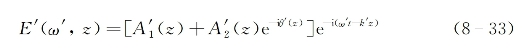
式中,![]() 为初始受激散射光(读取光)的实振幅函数,
为初始受激散射光(读取光)的实振幅函数,![]() 是读取波经过全息光栅形成的衍射波的实振幅函数,θ'(z)为表述后者波面特性的相位函数。
是读取波经过全息光栅形成的衍射波的实振幅函数,θ'(z)为表述后者波面特性的相位函数。
在小信号增益近似下,初始受激散射光沿行进方向上的变化为
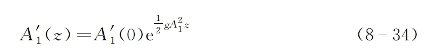
式中,g为指数增益因子。进一步假设在介质有效作用区内泵浦光的衰减可以近似忽略,则泵浦波场满足的波动方程为
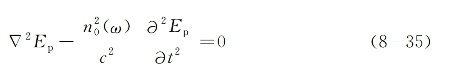
将式(8-32)代入上式可求得函数θ(z)满足方程:
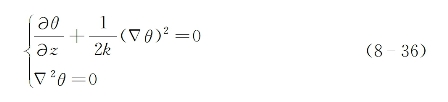
另一方面,经四波混频作用产生的衍射波![]() 满足的波动方程为
满足的波动方程为
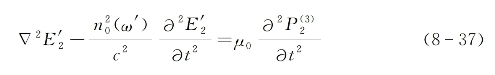
式中,μ0为真空中磁导率,![]() 是唯象引入的对应
是唯象引入的对应![]() 波的三阶非线性电极化波场,它可写为
波的三阶非线性电极化波场,它可写为
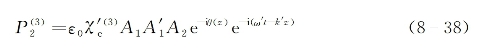
式中,![]() 是形式上引入的表征
是形式上引入的表征![]() 振幅增益的介质有效三阶非线性系数,因此可进一步表示为纯虚数形式,亦即
振幅增益的介质有效三阶非线性系数,因此可进一步表示为纯虚数形式,亦即![]() ,这里
,这里![]() 为实数。将式(8-38)代入式(8-37),然后利用振幅慢变化近似可求得
为实数。将式(8-38)代入式(8-37),然后利用振幅慢变化近似可求得
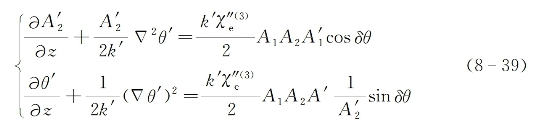
式中,
![]()
在像差影响不是十分大的情况下,θ'(z)的二阶导数可以忽略,故式(8-39)中第一式可以简化为
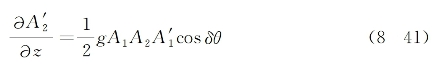
这里增益因子![]() 。另一方面,由式(8-36)中第一式减去式(8-39)中第二式后可得
。另一方面,由式(8-36)中第一式减去式(8-39)中第二式后可得
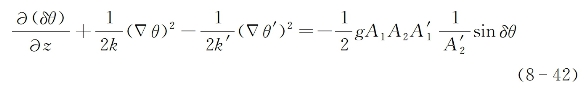
在小像差近似下,可认为θ和θ'的一阶导数的平方均十分小,以至于
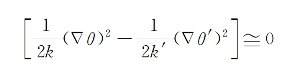
则式(8-42)简化为(https://www.xing528.com)
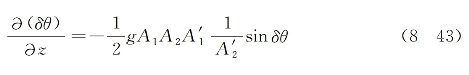
这样,得出相互关联的方程式(8-41)和式(8-43),它们共同描述![]() 波场的振幅与相位函数的变化规律。下面继续考虑它们的求解过程。
波场的振幅与相位函数的变化规律。下面继续考虑它们的求解过程。
首先,将式(8-41)被式(8-43)相除后可得
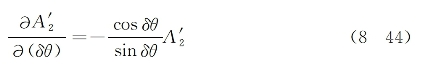
这一方程的解为
![]()
式中,B为一常数,而![]() (0)和δθ(0)为相应的初始值。由式(8-45)求得
(0)和δθ(0)为相应的初始值。由式(8-45)求得
![]()
将这一量再代入到式(8-41)后可得
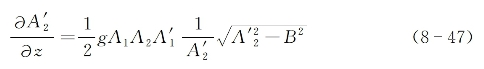
在衍射波出现的初始位置,![]() (0)值非常小以至于不管sinδθ(0)大小如何,总可以认为B≈0,则上面的方程进一步简化为
(0)值非常小以至于不管sinδθ(0)大小如何,总可以认为B≈0,则上面的方程进一步简化为
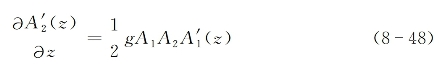
这里,已假设在弱波场振幅![]() 和
和![]() 获得指数增益的同时,强泵浦波场振幅A1和A2的变化可以近似忽略。式(8-48)的解为
获得指数增益的同时,强泵浦波场振幅A1和A2的变化可以近似忽略。式(8-48)的解为
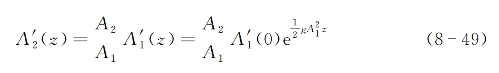
为进一步求解相位变化函数,可将式(8-49)代入式(8-45)求得
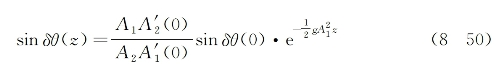
考虑到A1>>A2和![]() ,可认为上式中的分数项
,可认为上式中的分数项![]() 1,因此有
1,因此有
![]()
如果总的指数增益足够强,使得以下条件成立:
![]()
则有
![]()
上式的物理含义是,![]() 波在沿行进方向获得较强指数增益的同时,它的波面形状也越来越靠近A2泵浦波,但与后者的行进方向相反。
波在沿行进方向获得较强指数增益的同时,它的波面形状也越来越靠近A2泵浦波,但与后者的行进方向相反。
基于式(8-33)、式(8-34)、式(8-49)和式(8-53),由介质输出的总的后向受激散射波场可表示为
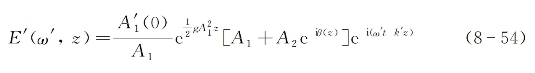
将其与由式(8-32)决定的总入射泵浦波场表达式相比较可以看出,总受激散射波场的确可以与总泵浦波场成相位共轭关系。这种关系存在的前提,是由式(8-52)决定的条件得到满足,亦即受激散射必须在远高于阈值的高增益实验条件下产生。
在多数受激散射实验情况下,泵浦光是以聚焦光束方式入射到散射介质中,此情况下的入射泵浦波场,可以用厄米高斯(Hermite-Gaussian)函数描述。采用同样的思路,经过类似但繁琐得多的数学推导过程,可以证明,在满足一定物理条件的前提下,总输出受激散射波场仍然可以与总输入泵浦波场成相位共轭关系[58]。所需要满足的条件,首先是单次通过介质样品的高增益,它决定于泵浦光强、介质增益因子与有效增益长度的乘积;其次是泵浦光经受的像差或畸变影响不能过大,否则受激散射输出波面的再现精度或保真程度将受到限制。这些推论,基本上与实验事实相符合。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




