对于简并四波混频产生相位共轭波的过程实质，可以用两种不同的物理机制加以解释：一种是四光子参量作用的机制，另一种则是全息光栅再现的机制。
首先考虑如何用四光子参量作用的机制来加以解释。一对行进方向相反的对撞泵浦光子在介质内湮灭前的动量之和为k1+k2=0，则按动量守恒要求，同时产生的分别属于E3和E4波场的另一对对撞光子动量之和也应满足k3+k4=0。对具有一定波面形状分布的信号波场来说，它可以看成是由一群行进方向略有不同的特定光子集合所组成。则按光子对撞产生的动量守恒要求，新生成的E4波场光子集合所决定的波面分布相对于它们的前进方向而言，必然呈现反转，从而使得E4波成为E3波的相位共轭波。正如第4章所讨论过的，四光子参量是一种基于电子云畸变的瞬时三阶非线性效应，所以要求E1，E2和E3波必须同时入射，而E4波的产生没有任何延迟。
再来考虑如何用全息光栅再现机制，来对如图8-4所示共轭波的产生加以解释［2，11］。该种解释的要点是，参与四波混频作用的一束泵浦光与入射信号光相互干涉并形成全息条纹，进而通过与光强成正比的折射率变化在介质内产生一种感应全息光栅，另外一束泵浦光作为读取光束在经过感应全息光栅的过程中，产生第4束能再现信号光波面（反转）信息的相位共轭光束。如图8-5所示，此情况下有两种可能的感应光栅对共轭波有贡献。
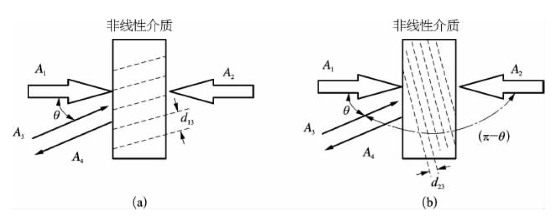
图8-5 利用简并四波混频产生后向相位共轭波时两种可能感应光栅的不同贡献
（a）A3与A1干涉形成的光栅；（b）A3与A2干涉形成的光栅
图8-5（a）是由信号光（A3）与成较小角度的泵浦光（A1）相互干涉形成的光栅贡献，该光栅的条纹平行于两光束夹角的角平分线方向，而条纹空间周期由两光束之间夹角确定：
式中，λ0为入射光在真空中的波长。图8-5（b）则是由信号光（A3）与近似反向的泵浦光（A2）相互干涉形成的光栅，其空间周期较小：
以图8-5（a）所示情况为例，相对于读取光A2而言，感应全息光栅的透过函数可唯象式地表示为
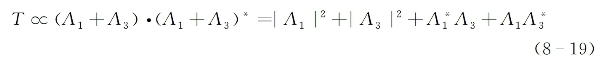
假设两泵浦光束为理想平面波，亦即有A2=
，则A2波经过光栅后的透射场可写为
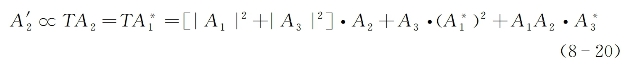(www.xing528.com)
式（8-20）右端第一项方括号项正比于A2本身，为不含空间信息的零级衍射波；第二项实际上包含了相位因子exp［-i（2k1·r-k3z）］，因一般不满足相位匹配，故不能产生有效的辐射；而第三项贡献代表读取光束A2经过光栅后的衍射波，也就是对应着我们感兴趣的含入射信号波空间相位信息的相位共轭波，为此可将其单独写为
另一方面，由前面用四波混频过程导出的式（8-12）中第二式可看出，在|γ|l＜＜1（介质为光学薄样品）时有
可见，由感应全息光栅再现模型也能给出与四波混频同样的物理结论。
虽然纯四波混频（或四光子参量作用）和感应全息光栅再现机理，均有可能对产生共轭波有所贡献，但是两种机理的物理本质是全然不同的。它们之间的最大区别是，四光子参量作用必须是同时的过程，而全息光栅的形成和波面再现却可以是非同时的过程。正如第5章所论述的，非线性介质折射率感应变化的物理机制是多样的，其中只有电子云畸变的机制是瞬时反应的，其他折射率变化机制均具有有限的响应时间和消失的弛豫时间。因此在如图8-5所示的光学安排下，可采用脉冲式的信号光和任意一束泵浦光同时入射并产生光栅，而另一脉冲泵浦光可在稍后的时刻入射。此情况下，四光子参量作用的可能已被排除，但由于残留全息光栅的存在，仍有可能观察到由读取泵浦光束产生的反向相位共轭光束。因此可以说，采用类似的读取光脉冲延迟入射的方法，可以很方便地判断所观察到的相位共轭波的产生物理机制。到目前为止的研究表明，绝大多数通过四波混频实验观察到的相位共轭波，均出自全息光栅再现的物理贡献。
以上数学推导和说明，都隐含了参与混频作用的4种光波均具有相同频率和偏振方向的假设。下面进一步说明，在其他的偏振状态和频率组合条件下，也同样可获得后向相位共轭波。
首先考虑三种频率相同入射光波的不同偏振状态组合对相位共轭波偏振特性的影响。采用全息光栅的模型，可以比较简明地说明这个问题。
假设三种频率相同的光束线偏振光的取向，按如图8-6所示三种不同组合方式入射。其中图8-6（a）表示三种入射波均以s偏振方式进入介质，则共轭波A4亦为s偏振；图8-6（b）表示A1和A3波以s偏振入射，读取A2波以p偏振入射，则共轭波A4亦为p偏振；图8-6（c）表示A2和A3波以s偏振入射，读取A1波以p偏振入射，则共轭波A4亦为p偏振。类似的分析，可推广到其他更为复杂的入射偏振（如圆偏振或椭圆偏振）组合的情形。此外应注意到，在图8-6（a）所示情况下，有两种全息光栅的贡献同时起作用；而在图8-6（b），（c）所示情况下，则只有一种全息光栅的贡献在起作用。
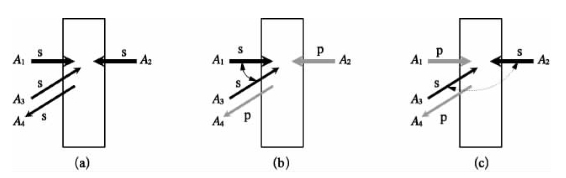
图8-6 利用简并四波混频产生后向相位共轭波时偏振态组合的影响
（a）3种入射光束具相同s态偏振；（b）A1和A3波具相同s态偏振；（c）A2和A3波具相同s态偏振
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
