SRBS产生的阈值条件-《非线性光学与光子学》

如图7-36所示，在所考虑的双光子吸收介质内，由沿z轴方向行进的单色平面泵浦光与反向瑞利散射光相互干涉产生的驻波场光强的周期性分布可表示为

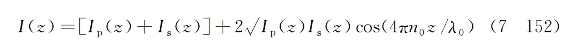
式中，Ip为泵浦光强，Is为反向散射光强，λ0为泵浦光在真空中的波长。介质内感应折射率变化的空间周期性起伏可相应写为

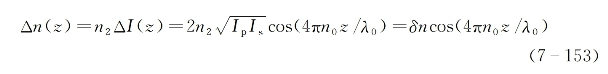
式中，n2为散射介质的非线性折射率系数，而折射率的调制幅度为

由上述折射率空间周期性调制形成的厚度为L的相位光栅的反射率可表示为［143］

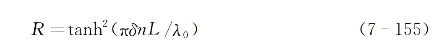
将式（7-154）代入上式可得

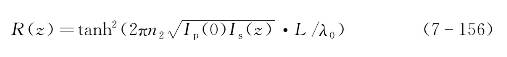
来看反向受激散射刚产生时的阈值情况，为简单计，仍然假设入射泵浦光强在此时由双光子吸收等机制造成的衰减可近似忽略，亦即Ip（z）≈Ip（0）。另外考虑到在阈值附近反向受激散射光强仍然远小于泵浦光强，故感应光栅的反射率远小于1，因而由式（7-156）表示的双曲正切函数可以近似用该函数的变量值来代替，从而有

(www.xing528.com)

从上式可看出，光栅反射率是介质内位置z的函数。可按以下方式定义一个在阈值水平附近进行泵浦时的光栅平均反射率：

式中，Is（L）为反向瑞利散射光（种子信号）的初始光强，Is（0）为阈值时在样品入射端面的反向受激散射的输出光强。

参见图7-36，在泵浦达到阈值时，考虑到除光栅反射以外的其他可能损耗机制，来自泵浦光反射的能量应等于或大于由入射面反向输出的受激散射能量，亦即

将式（7-158）代入式（7-159）后可得对泵浦光强的阈值要求为

式中

代表在阈值附近泵浦时，介质反向瑞利散射信号的单程光强放大倍数。对所有发生在纯净介质中各类受激散射过程而言，其初始的自发散射（种子）信号都十分微弱，其光子简并度≤10-2量级，而阈值附近能探测到的受激散射信号光子简并度在106～108量级，故相应的单程光强放大倍数在108～1012量级范围［144，145］。

从式（7-160）出发可引申出如下的物理推论，受激瑞利布拉格散射易于在具有较大n2值的介质中产生，亦即需要折射率变化的多光子共振增强。这里应注意到，以染料溶液为例，n2值与具有多光子共振能力的染料分子浓度成正比。