实验结果与理论比较：非线性光学与光子学

1）CS2液芯光纤前向受激散射结果

利用上面介绍的受激克尔散射的物理模型和基本公式，可以对出自充有克尔液体的空心光纤系统的超宽带受激散射实验结果（见图7-28）给出一种合理的解释。首先，由描述分子微分散射截面的基本公式（7-132）和式（7-138）可见，由于对大多数克尔液体来说，瑞利克尔散射及拉曼克尔散射的概率远小于普通瑞利散射及拉曼散射的概率，因此只有在具有较长增益长度和高泵浦光强条件下，才容易观察到受激克尔散射效应的充分出现。而充有克尔液体的空心光纤系统，正好符合这些要求。对于由图7-28（a）所示充有CS2液体的情况来说，可认为分子的普通极化率各向异性以及拉曼极化率各向异性都比较大，因此可同时观察到受激瑞利克尔散射以及受激拉曼克尔散射的出现。对于由图7-28（b）所示的充有C6H6液体的情况来说，可认为分子的普通极化率的各向异性并不很大，但其拉曼极化率的各向异性却很大（这可由已见报道的拉曼增强的光克尔效应的研究所证实），因此在空心光纤条件下，比较容易观察到附加在各级SRS谱线低频一侧的受激拉曼克尔散射效应的出现。对由图7-28（c）所示充CCl4液体的情况来说，由于分子具有四面体结构，因此近似为各向同性分子，故受激克尔散射效应很难观察得到。

接下来着重考察由液芯光纤输出的前向受激克尔散射的光谱特性、由普通液盒输出的反向受激克尔散射的光谱特性。

图7-31为不同泵浦光强水平下，出自CS2液芯光纤受激瑞利克尔散射的光谱分布曲线。所用空心光纤之内径为100 μm、长约2.5 m，入射激光波长532 nm、脉冲宽度10 ns、光谱宽度约0.9 cm-1，用高分辨率大型双光栅单色仪和光学多通道分析仪进行光谱测量和记录，系统光谱分辨在入射光波长附近为0.4cm-1［16］。

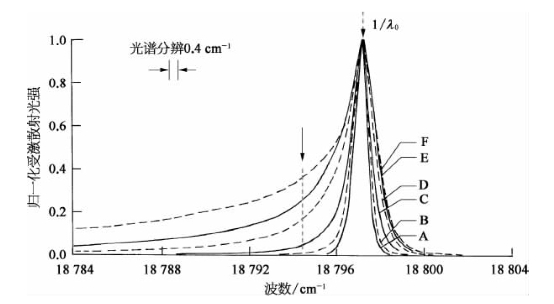
图7-31　不同光泵水平下，出自2.5 m长充CS2液芯光纤输出前向受激瑞利克尔散射的光谱分布曲线（A—1.3 MW/cm2，B—3.9 MW/cm2，C—13 MW/cm2，D—39 MW/cm2，E—130 MW/cm2，F—390 MW/cm2，泵浦波长λ0=532 nm，光谱峰值左方虚线标示出受激瑞利翼散射理论预计的极大值位置）［16］

由图7-31可见，随着光泵水平的提高，受激散射向入射光谱线两侧的非对称光谱展宽程度增大，但在低频移一侧，从未观察到由受激瑞利翼散射理论公式（7-122）所预测的光谱分布极大值（图中以垂直虚线标示）。实验结果表明，对于给定的液芯光纤长度而言，当入射光泵水平提高到一定程度之后，受激散射的相对光谱分布不再继续发生明显的变化，亦即达到其饱和的展宽分布；这意味着对应于具有不同初始取向角分子的克尔散射增益，都已达到满足由式（7-148）所表示的受激散射的阈值条件。

根据式（7-146），受激瑞利克尔散射归一化增益函数可表示为

f（Δv）是一个待定的未知函数，作为一种试探，可唯象式地假设其具如下的简单形式：

式中，A和B为由实验结果确定的与具体介质有关的数值系数。

在与图7-31相同实验条件下测得的受激瑞利克尔散射归一化增益函数曲线如图7-32中的细实线所示；而利用式（7-149）和式（7-150）所作最佳拟合曲线由粗实线所示，所采用的最佳拟合参数为

图7-32　在I0=270 MW/cm2泵浦水平下，出自CS2液芯光纤之前向受激瑞利克尔散射的归一化增益光谱曲线［16］

这里，受激散射频移Δv以cm-1为单位，而f（Δv）以角度度数为单位。作为对照，在同一图中用虚线给出了由式（7-122）给出的受激瑞利翼散射理论曲线，该曲线与实验结果明显不符合。

以上是采用10 ns脉冲激光和充CS2液芯光纤所获得的结果，稍后在大致相同实验条件下使用不同脉冲宽度（20 ns，4 ps，0.5 ps）激光泵浦，均得到与以上所述基本相同的前向受激瑞利克尔散射结果［130～132］。

2）苯液芯光纤前向受激散射结果(www.xing528.com)

在相同实验安排条件下，以充苯的液芯光纤代替充CS2的液芯光纤，所测得的前向受激散射光谱加宽行为，亦有明显的不同。图7-33给出了在不同入射泵浦光强水平下，测得的前向输出相干辐射光谱分布曲线［129］。其中图7-33（a）为不同输入光强水平下在泵浦光谱线附近的光谱光强分布，而图7-33（b）为在苯的第一级受激拉曼散射谱线附近的光谱光强分布。由该图可以看出，在入射泵浦光强高至300 MW/cm2的条件下，在泵浦光谱线附近的非对称光谱加宽基本不明显，这表明液态苯分子在处于基能态时的光学各向异性与CS2分子相比不够大，因此相应的受激瑞利克尔散射的增益不够高。但与此同时，在相同的泵浦光强范围内，却在苯的受激拉曼散射谱线的低频一侧，观察到明显的具有连续光谱红移的受激散射贡献。这一事实表明，苯分子在处于振动激发态时，其光学各向异性明显增大，因此可提供较高的受激拉曼克尔散射增益。

图7-33　不同光泵水平下，出自2.5 m长充苯液芯光纤前向输出光谱分布曲线［129］

（a）泵浦光谱线附近光强分布；（b）第一级受激拉曼散射谱线附近光强分布（泵浦光强水平：A—3 MW/cm2，B—9 MW/cm2，C—30 MW/cm2，D—90 MW/cm2，E—300 MW/cm2）

3）CS2液盒后向受激散射结果

虽然受激瑞利克尔和拉曼克尔散射的早期发现，是通过具有高增益的液芯光纤系统的前向输出实现的，但这两种效应在普通激光实验室条件下，同样可利用长度为厘米量级的充有克尔液体的液盒，由后向观察到。由后向进行观测的好处是可以避免前向透过泵浦光的强背底影响。

图7-34给出了在时宽为10 ns、波长为532 nm的脉冲激光泵浦下，出自10 cm长CS2液盒的后向受激散射的光谱照片。图7-34（a）是在入射泵浦光具有1 cm-1光谱宽度条件下获得的，而图7-34（b）则是在入射光具有0.1 cm-1光谱宽度条件下获得的［133］。

图7-34　在10 ns和532 nm激光脉冲泵浦下，出自10 cm长CS2液盒的后向受激散射的光谱照片［133］

（a）泵浦线宽为1 cm-1；（b）泵浦线宽为0.1 cm-1（泵浦光强为150 MW/cm2，光谱分辨为9 cm-1）

在图7-34（a）所示情况下，再一次看到受激瑞利克尔散射的连续低频移光谱分布，与前面叙述过的CS2液芯光纤的前向受激散射输出光谱分布一致。但在如图7-34（b）所示窄谱线泵浦情况下（泵浦光强相同），却只看到分别出现在泵浦线（λ0）和CS2 一级受激拉曼散射线（λS1）位置处的两个光谱峰值，而在它们低频一侧的受激克尔散射贡献则并不明显。由图7-34所示后向受激散射光谱行为与泵浦光谱线宽度有关的实验事实，可以用不同种类受激散射之间的竞争来加以解释。通过7.2节与7.5节的理论描述已经知道，受激拉曼散射与受激布里渊散射的产生阈值，均随泵浦光谱线宽度的减小而降低。在如图7-34（a）所示使用较宽谱线宽度泵浦条件下，对CS2液盒而言，受激瑞利克尔散射的产生阈值最低，故能优先产生宽频移的受激散射并进一步压制其他的受激散射机制。而在如图7-34（b）所示情况下，由于入射谱线变窄了十倍，受激拉曼散射与受激布里渊散射的阈值明显降低，因此它们可比受激克尔散射优先产生，并相对地占据主导地位。近期发表的有关在CS2液盒中，以上三种反向受激散射竞争相对于泵浦线宽依赖性的详尽研究［134］，进一步证实了上述的分析结论。

图7-35为在与图7-34（a）基本相同的实验条件下（泵浦光强为500 MW/cm2），测得的CS2后向受激散射归一化增益分布曲线（实线）、受激瑞利克尔散射理论拟合曲线（虚线和点划线）［图7-35（a）］以及受激瑞利翼散射理论拟合曲线（短划线）［图7-35（b）］之间的比较。两种理论拟合所采用的德拜时间值均为与实测值接近的τ=1.5 ps。

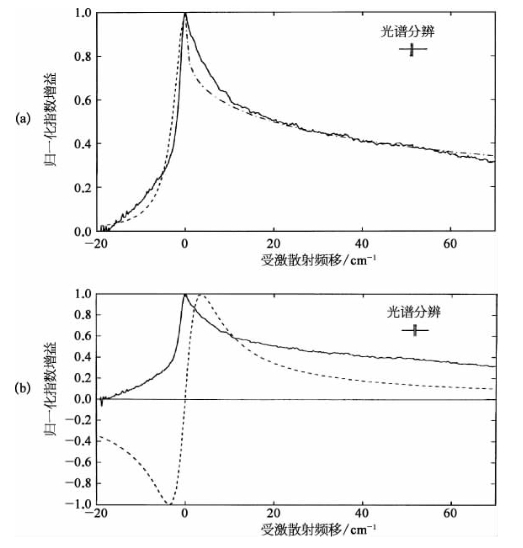
图7-35　在与图7-34（a）基本相同实验条件下测得的CS2后向受激散射归一化光谱增益曲线（实线）、与受激瑞利克尔散射理论拟合曲线（虚线和点划线）

（a）以及受激瑞利翼散射理论拟合曲线（短划线）（b）的比较（所采用的德拜时间值为τ=1.5 ps，光谱分辨为0.48 cm-1）［133］

图7-35的高分辨增益光谱的实验曲线清楚表明，在泵浦波长的高频一侧，也存在着由德拜时间倒数值（测不准关系）决定的光谱加宽。而这与图7-35（b）所示受激瑞利翼散射理论的预计完全相反。

由克尔散射的基本物理模型出发，也可进一步解释普通弱光激励下观察到的瑞利翼散射的实验规律性。通过开展对普通（自发）和受激克尔散射的基础研究，可加深人们对液体介质内各向异性分子在光场作用下再取向动力学过程的了解。而受激克尔散射的实际应用意义，是向人们提供了一种产生超宽带相干光辐射的新途径，同时也提供了对宽谱带弱输入光信号进行受激散射放大的新的有效方法［123，131，135，136］。