图7-30 液体内各向异性分子感应电偶极矩矢量p与光场矢量E以及与分子最大极化率方向（z轴）之间的夹角关系
本小节将从已知的分子拉曼散射截面的普适公式出发，在考虑到组成克尔液体的分子感应极化各向异性的特殊情况下，分别求出瑞利克尔和拉曼克尔散射截面的表达式。
如果液体分子为光学各向异性，则可以从式（7-45）出发，进一步导出描述拉曼克尔散射截面的表达式。
如图7-30所示，假设入射光场E为线偏振，偏振方向上的单位矢量为e0；散射分子具两维方向上的各向异性，z和x轴分别为分子最大和最小极化率轴；e'为分子感应电偶极矩p方向上的单位矢量。由于分子对光场的各向异性的反应，使得p和E一般并不同方向，它们与z轴夹角分别为α和θ。在这种情况下，式（7-45）中的偶极矩阵元乘积项可表示为
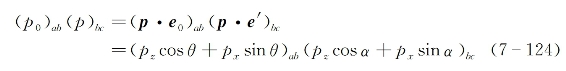
式中，所含两个角度α和θ彼此并不独立，利用分子极化率的半经典理论，可将其中一个消除。在半经典理论中，分子感应偶极矩矢量p沿x轴和z轴的分量为
px=αxxEx
pz=αzzEz
式中，Ex和Ez是E的投影分量，αxx和αzz是分子极化率张量元。由图7-30有
Ex=|E|sinθ
Ez=|E|cosθ
因此有
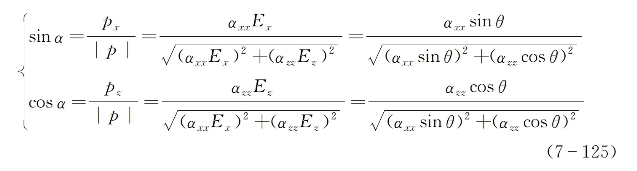
式（7-125）意味着角α系由分子取向角θ以及分子的各向异性所决定。只有当αxx=αzz（各向同性）时α=θ，否则α≠θ。将式（7-125）代入式（7-124）后可得到只含有角度θ的表达式：
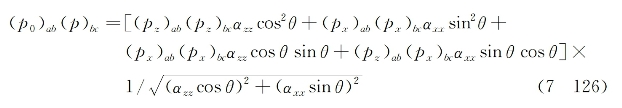
另一方面，在入射强光场作用下，克尔液体内分子的取向统计分布函数F（θ）按式（5-39）可写为
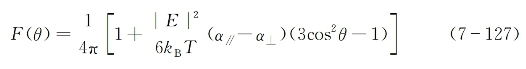
式中，α//=αzz，α⊥=αxx，kB是波尔兹曼常数，T为绝对温度。式（7-127）意味着分子按光场偏振方向而言，可呈现出两组对称的分布：一组具有+θ角，另一组具有-θ角。设散射分子密度为N而入射光在介质内的作用区体积为V，则所有具相同|θ|取向角的分子集合的总散射概率正比于式（7-45）按NVF（θ）个分子的求和。这种求和的结果，是使式（7-126）右端方括号中前面两项加倍，而后面两项相互抵消。因此式（7-126）可以简化为
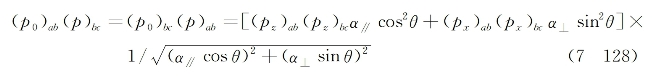
基于式（7-128）和式（7-45），对克尔液体而言，细致化后的各向异性分子的拉曼散射截面可写为
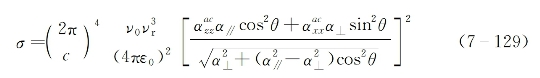
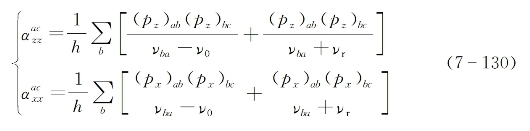(www.xing528.com)
式中，
分别是表征分子由能级a至能级c的拉曼跃迁的分子极化率张量元。如果假设分子极化率的各向异性不是很大，则式（7-129）可改写为
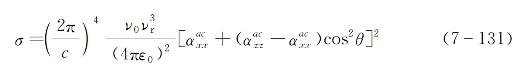
进一步考虑到上式方括号中第二项远小于第一项，则该式可最后简化为
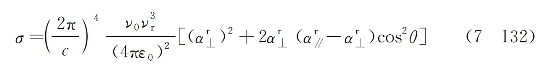
式中，
为分子的各向异性拉曼极化率。在式（7-132）右端方括号中的第一项对应与θ无关的普通拉曼散射贡献，第二项对应与分子各向异性和取向角变化有关的拉曼克尔散射贡献。后者的散射截面可单独写为
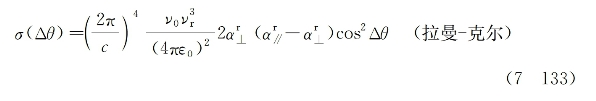
式中，Δθ=θ0-θ'=θ代表分子在完成散射过程前后的取向角变化，它的大小决定了分子再取向所做的功（W）或散射光的频移大小，亦即
虽然不知道Δθ与Δv之间的确切关系，但可唯象地假设：
式中，f（Δv）是一种随Δv而正变的待定函数，其具体形式与介质有关，并可通过实验加以确定。基于这种考虑，式（7-133）可改写为如下散射频移的函数形式：
对瑞利散射而言，a=c，vr=v0，因此有
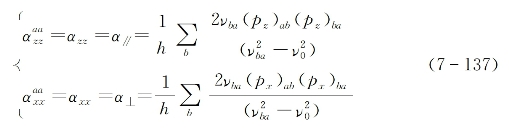
这样，可直接从式（7-129）得出克尔液体各向异性分子的瑞利散射截面为
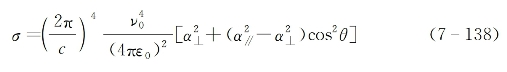
式（7-138）右端方括号中的第一项对应与θ无关的普通无频移的瑞利散射贡献，第二项对应与分子各向异性和取向角变化有关的瑞利克尔散射贡献。后者的散射截面可单独写为
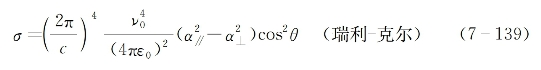
式（7-139）也可改写为如下的与散射光频移有关的函数形式：
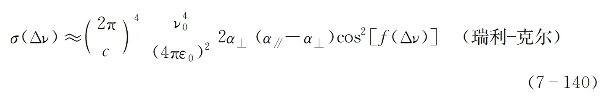
知道了组成液体的各向异性分子的克尔散射截面，就可进一步求出与入射泵浦光强有关的指数增益特性。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
