克尔散射的物理模型-非线性光学与光子学

从20世纪80年代后期到90年代初，He等人对在CS2和C6 H6中发现的超宽带受激散射现象，继续进行了深入的系统研究。在所获得的精度更高的定量测量数据的基础上，先后提出了受激瑞利克尔散射和受激拉曼克尔散射的物理模型，从而可对至今为止观察到的有关超宽带受激散射现象的主要实验规律性，给出一种较为统一的解释［16，129］。所提出的受激克尔散射理论的基础，是把光频克尔效应（光场引起的各向异性分子的感应再取向），在本质上看成分子对入射光的一种频移散射效应。借助有关光散射的量子理论描述方法，可对克尔散射效应的两种微观机制，给出非常简洁的物理说明。假设由各向异性分子组成的纯净液体介质，对入射光场而言，是完全透明的，亦即不存在任何意义上的本征共振吸收。在由入射强光场引起分子感应再取向的过程中，为克服转动阻尼作用，分子必须从入射光场中获得部分额外的能量；但由于不存在共振吸收，因此能量由光场向分子的转移，只能以分子对入射光的红移散射方式进行。具体的基元散射过程，如图7-29所示。

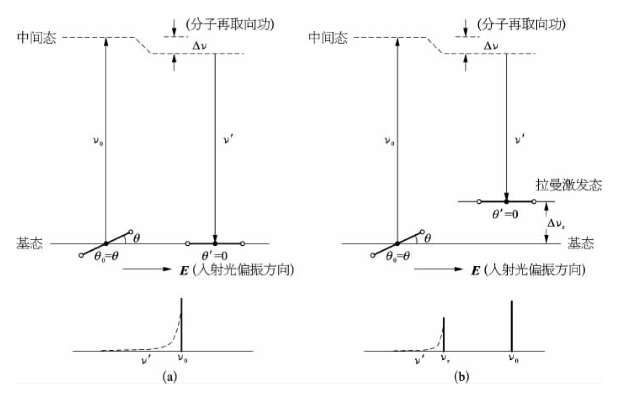
图7-29　液体内各向异性分子克尔散射基元过程的跃迁

（a）瑞利克尔散射；（b）拉曼克尔散射

以CS2这类分子为例，在图7-29（a）所示情况下，一个相对于入射光场（E）偏振方向而言初始取向角为θ0=θ≠0的各向异性分子，可通过一个入射光子（频率为v0）的湮灭和一个红移散射光子（频率为v'）的产生，而获得额外的能量去完成按光场偏振方向上的重新取向，终止取向角为θ'=0。假设在这一基元散射过程的始末，分子一直处于其基态本征能级，则分子由光场获得的能量为hv0-hv'=hΔv，这一能量最后转换为分子在完成再取向过程中为克服转动阻力所做的功，后者的大小又与始末取向角的变化量Δθ=θ0-θ'=θ的大小有关。考虑到具有不同初始取向角的分子为完成按光场偏振方向上的再取向而需要不同的额外能量，因此散射光的频移量也相应有所不同，最后在宏观上有可能观察到附加在入射光谱线低频一侧的连续频移散射谱。图7-29（b）所示基元过程与上述过程基本相似，唯一不同之处，是散射分子在完成再取向过程的同时，跃迁到其某一拉曼激发能级，此情况下该分子由光场获得的能量为h（Δv+Δvr）；这里Δvr为拉曼跃迁频移，Δv为散射光频率相对于拉曼散射跃迁中心频率vr的相对移动。大量分子按图7-29（a）所示的微观过程所给出的宏观结果，是在入射激光谱线的低频一侧，出现连续频移散射光谱，可称之为瑞利克尔（Rayleigh-Kerr）散射。而图7-29（b）所示的散射过程的结果，是在介质拉曼散射谱线的低频一侧，出现连续频移散射光谱，可称之为拉曼克尔（Raman-Kerr）散射。(www.xing528.com)

按能量守恒的要求，分子再取向所做的功W与克尔散射光的频移之间应满足如下关系式：

式中，W应该是散射分子取向角变化量Δθ的一种正变函数，可以想象到大的取向角变化，需做较大的再取向功，从而应伴随着较大的散射光频移。

本节后面的论述将会表明，如同普通拉曼散射一样，在强相干光场泵浦作用下，克尔散射亦可获得指数增益，并在满足阈值条件的情况下，最终成为超宽带受激散射光输出。用受激瑞利克尔散射的模型，可以解释如图7-28（a）所示CS2液体给出的实验结果，亦即何以在泵浦光波长的低频一侧出现超宽带受激散射；而用受激拉曼克尔散射的模型，可以解释如图7-28（b）所示C6H6液体给出的结果，亦即何以仅在SRS谱线的低频一侧出现超宽带受激散射。