布里渊散射,是指入射光波场与介质内弹性声波场之间相互作用而产生的一种散射现象。其主要特点,是散射光的频率相对入射光频率发生变化;这种频移量的大小,则与散射光方向以及介质内的声速特性有关[6]。
众所周知,当一定频率的单色光入射到衍射光栅上时,将在某一些特定方向上产生衍射极大值,而当这种光栅处于运动状态时,则除了在特定方向上产生衍射极大值外,还将由于多普勒效应而引起衍射光频率的变化;频率变化的大小,则与光栅的运动速度和方向有关。如果以一个充有某种介质的超声盒代替光栅,由于超声振动的结果,引起介质密度(从而也是折射率)随时间和空间的周期性起伏,因此超声振动介质本身相当于一个运动着的光栅:当一束单色定向光束通过它时,将在某些确定的方向上产生频率移动了的衍射极大值,衍射光的方向和频移量的大小,自然与介质内的超声波场特性(如运动速度和方向)有关。
在一般情况下,任何光学介质内部均存在着由大量质点统计热运动所形成的自发的弹性力学声波场,这种声波场可分解为无数多单色简谐平面声波之和,每一种单色平面声波场将引起介质密度随时间和空间的周期性变化,因此将引起对入射光波的“衍射”效应。“衍射”光的频率将随声波场的速度和传播方向的不同而产生变化,这就是普通布里渊散射的经典物理图像。介质内由自发热运动产生的弹性声波场总是十分微弱的,加上在激光技术出现前又缺乏高单色定向亮度的光源,因此使得对普通布里渊散射现象的观测比较困难,从而也限制了布里渊散射技术的发展。
激光技术出现后,当以高单色定向亮度的激光束入射到为数相当多的不同光学介质中时,不但可以产生很明显的布里渊散射效应,而且在一定条件下,可使这种散射过程具有一系列崭新的特点(如高增益性、阈值性、定向性、可实现持续振荡、可调谐性等),这就是所谓受激布里渊散射过程[14]。
普通与受激布里渊散射的本质区别,在于前者是由介质内的自发弱声波场引起的,而后者则是介质内由激光电致伸缩作用产生的强感应声波场对入射光的作用引起的。在强光作用下,由于光频电磁场电致伸缩效应(在外电场作用下介质产生周期性形变或弹性振动)开始变得明显,从而可使介质内某些状态的声波场得到极大增强,以至于当介质内的电致伸缩声波场和相应的散射光波场的增强作用大于它们各自的损耗作用时,将出现声波场与散射光波场的相干放大或持续振荡,这就是受激布里渊散射效应的经典物理图像。从场的量子理论出发,可以对受激布里渊散射给出更简明的描述。此时可把这种过程看成光子场与声子场之间的散射过程,亦即入射光子、散射光子、声子三者之间的参量作用过程。在作用过程中,应满足能量守恒与动量守恒,并且以下述两种可能的方式进行。
1)斯托克斯散射光的形成
此过程可表为一个入射光子的湮灭以及一个感应声子(通过电致伸缩机制形成)和低频散射光子的同时产生。其能量和动量守恒要求为

式中,v0,vs,va分别为入射光子、散射光子、感应声子的频率,而k0,ks,ka分别为三种波量子的波矢。可以看出,这种散射过程的特点,是一部分入射光能量转变为介质内的感应声波场能量。为求出散射光频移量的大小,可按图7-20所示的波矢耦合条件去进行考虑。由式(7-78)可以看出,由于声波频率远小于光波频率,va<<v0,vs,故可认为v0≈vs和k0≈ks,则由图7-20不难看出在满足式(7-78)第二个条件的情况下,应近似有

式中,ka=2π/λa=2πva/υa,k0=2πn/λ0=2πnv0/c;λ0和λa分别为入射光子和声子的波长;c/n和υa分别为介质内光子和声子的速度;n为介质折射率;θ为所考查的散射光相对于入射光的夹角。
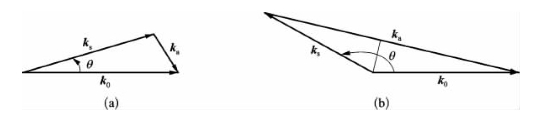
图7-20 斯托克斯频移布里渊散射的波矢耦合条件
(a)向前方的散射;(b)向后方的散射
基于式(7-79)和式(7-78)中第一个方程,可以得出散射光频移表达式为(https://www.xing528.com)
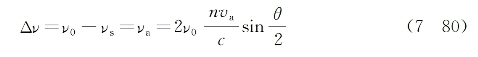
由上式可以看出,当散射角θ=π时(反向散射),斯托克斯散射光的频移为最大。

实验中,可利用法珀干涉仪或光电外差方法精确测量散射频移值,从而可间接确定介质内的声速υa的值。由图7-20还可以看出,对θ=π的反向散射来说,波矢耦合是按共线方向实现的,亦即声波场与入射光同向而与散射光相反。
2)反斯托克斯散射光的形成
此过程可表为一个入射光子和一个强声波场声子的湮灭,以及一个高频散射光子的同时产生。这种过程满足的能量和动量守恒要求为

式中,vas和kas分别是高频移散射光的频率和波矢。可以看出这种过程的特点,是介质内已经产生的强声波场将其一部分能量转移到散射光之中,从而使散射光频率变高。
由波矢耦合图7-21可看出,反斯托克斯光相对于入射光的频移值亦为

同样由上式可见,当θ=兀时散射光频移值为最大。此时,介质内强声波场的方向同入射光方向相反。
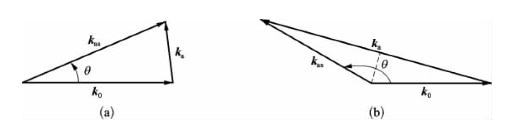
图7-21 在介质内已经存在强声波场情况下,反斯托克斯频移布里渊散射的波矢耦合条件
(a)向前方的散射;(b)向后方的散射
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




