受激拉曼散射增益系数与阈值条件来自《非线性光学与光子学》

下面将在以上公式的基础上，进一步求受激拉曼散射的指数增益系数。式（7-48）中W（t）是指单位时间内NgV个分子在某一入射波型内个光子作用下向Ω0立体角范围内散射出一个光子的概率。考虑到实际的入射光场总是由多个波型组合而成，波型数目由入射光立体发散角Ω0、光束截面S0、光谱宽度Δv0所决定，而在单位时间内通过相互作用区的入射波型数乘上每个波型内的光子数，正好等于P0/hv0（P0为入射光功率）。考虑到上述因素后，由式（7-48）出发，可将单位时间内总的受激散射光子数的增加速率写为

式中，P'为受激散射光的总功率。设入射光束截面S0与受激散射光束截面S'近似相同，并忽略v'与v0的差别，则上式可改写为

式中，I0与I'分别为入射光与受激散射光的总光强。设受激散射光的平均单色光强为I（v'），平均谱线宽度为，则有。此外，考虑到受激散射光子简并度与单色光强的下述关系［参见式（1-13）和式（1-24）］：

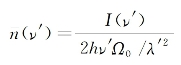
式中，λ'为在介质中散射光的波长，则式（7-50）可进一步化简为

为简单计，这里只考虑稳态受激散射的情况，亦即过程涉及的所有物理量都与时间无显函数关系。此种情况下，可将I（v'）随时间的变化理解为沿光行进方向（z轴）上的增长变化。为此，可在式（7-51）中令dt=dz/c'而得

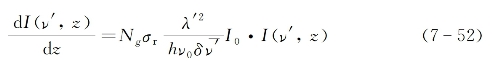
将上式完成对z的积分后可得

式中，指数增益系数G（单位是cm-1）为

在求出上式的过程中，采用了小信号近似，亦即入射泵浦光强在所考虑的传输长度上的减弱可以忽略，故I0可近似看成常数。从这样求得的公式（7-54）中可以看出，受激拉曼散射的指数增益系数G分别与散射过程初始能级上的分子密度Ng、散射截面σr、泵浦光强I0成正比，而与受激散射的光谱宽度成反比。

到目前为止，还没有考虑受激拉曼散射的光谱结构以及入射泵浦光谱宽度对增益的影响问题。这里可分为两种极端情况加以简化考虑。首先考虑入射泵浦激光谱线宽度远小于自发拉曼散射的谱线宽度的情况（实际实验条件大都如此）。此时受激拉曼散射的谱线宽度和形状主要是由自发拉曼谱线的线型分布所决定，而式（7-54）可改写为

式中，S（v'）为描述自发拉曼散射谱线分布的归一化线型因子，其量纲与相同。假如自发拉曼散射光谱具有洛伦兹线型，则S（v'）可表示为

式中，v0与v'分别为入射光和拉曼散射光的频率，Δvr为拉曼跃迁中心频移值，而δv'为自发拉曼谱线半峰全（频率）宽度。

其次，再考虑另外一种极端情况，亦即入射泵浦光谱线宽度远大于自发拉曼线宽。此情况下，受激拉曼散射的谱线分布主要由入射泵浦光的谱线分布所决定，而相应的与频率有关的指数增益因子可改写为(www.xing528.com)

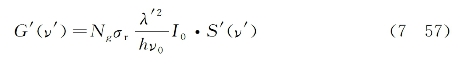
式中，S'（v'）为描写泵浦光谱线分布的归一化线型因子。假设它也具有洛伦兹分布线型，则有

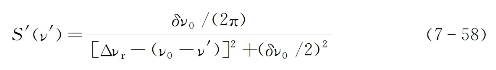
式中，δv0为泵浦激光谱线半峰全（频率）宽度。根据式（7-55）和（7-57），上述两种情况下的增益系数极大值之比为

由此可见，以具有比自发拉曼线宽窄得多的激光谱线进行泵浦，更容易产生受激拉曼散射。这一结论可以解释为何采用纳秒脉冲激光，比采用飞秒脉冲激光更容易产生受激拉曼散射，因为前者的光谱宽度显著小于后者。

至此，一直假设拉曼散射过程的起始与终止能级只有两个（g和f，见图7-2）。设能级g为较低的能级，则上面推导出的公式适用于斯托克斯散射的情况。设较高能级f上的分子数密度为Nf，则同样可导出反斯托克斯受激拉曼散射的指数增益系数为

式中，G由式（7-54）给出。通常Ng＞＞Nf，因此有G＞＞Gas，故斯托克斯受激拉曼散射更容易被观测到。然而，在某些实验情况下，当激光泵浦作用足够强，通过受激斯托克斯过程有足够多的分子被激励至拉曼激发态f，使得Nf获得显著增加，则同样可观测到反斯托克斯受激拉曼散射。

如果实际的介质存在着更复杂的能级结构，使得在其不同本征能级之间同时允许有多种拉曼散射跃迁（其中之一相当于前面所述分子由能级g至f的跃迁），则在足够高的入射光激励水平下，有可能同时产生多种不同拉曼频移值的受激散射，但对其中任何一种给定频移值的受激散射过程来说，本节上面给出的理论与公式描述完全适用。考虑到拉曼散射光在介质本身传输过程中不可避免地受到多种损耗因素的影响，如杂质吸收、其他形式的散射损耗等；而向一个给定波型内的散射概率又直接与该波型内已有的散射光子数有关。以上两个因素在本质上就决定了该过程的发生，具有明显的阈值性，这同激光的产生具有明显的阈值性是同样的原因。

对于有共振腔情况下的受激拉曼散射，阈值条件为

式中，α为散射介质对于散射光而言的衰减系数，L为散射介质的增益长度，R为共振腔反射镜的反射率。对于单次通过散射介质的行波放大式受激拉曼散射而言，阈值条件为

由以上两式的比较可以看出，在有腔情况下的受激散射阈值要求较低，因此适用于入射光激励水平较低、散射截面较小、增益长度较短的场合；而单次行波放大的阈值条件则要求较高，因而适用于高激励水平、散射截面较大、介质增益长度较长的情况。

为表征在同样实验条件和泵浦光强水平下，不同介质产生受激散射的难易程度，可将式（7-54）增益系数的一般表达式改写为

式中，引入的gs为给定介质的拉曼散射指数增益因子（单位是cm/MW）：

在假设入射泵浦光谱线宽度δv0远小于自发拉曼线宽δv'的情况下，有≈δv'，则gs是只与介质材料有关的物理量。