光谱自加宽-非线性光学与光子学

按照傅里叶分析原理，一种快速的相位调制，必然伴随着光谱的相应加宽。为求出加宽后的光谱能量分布，可对经受相位调制后的光场进行逆傅里叶变换［参见式（2-48）］：

式中，Δφ（t）∝|E0（t）|2由式（6-39）所决定。上式可改写为

式中，Δω=ω-ω0表示由自相位调制跃迁引起的频率移动。进而可将光强按光谱分布写为

作为一个定量的实例，仍然假设准单色入射脉冲具高斯状时间波形，半宽度为τ，最大相移量为Δφmax，则根据式（6-47）和式（6-48），可求出不同入射参数条件下如图6-13所示的脉冲光谱自加宽分布曲线。从该图可看出一些规律：

(www.xing528.com)

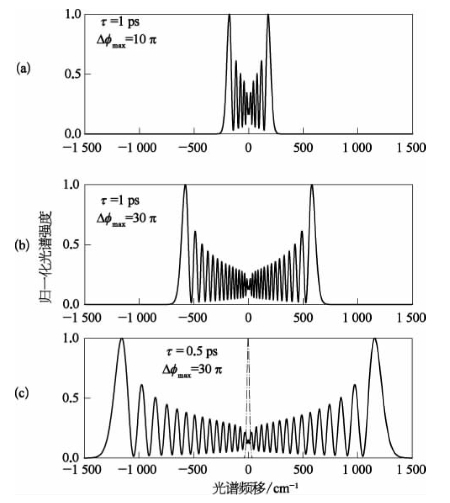
图6-13　不同条件下的脉冲光谱自加宽曲线

（a）脉宽τ=1 ps，最大相移Δφmax=10π；（b）τ=1 ps，Δφmax=30π；（c）τ=0.5 ps，Δφmax=30π（其中点划曲线表示由傅里叶变换限定的入射脉冲初始谱宽）

（1）在脉宽相同的前提下，光谱加宽范围与最大相移量Δφmax成正比。

（2）在最大相移量Δφmax为相同的前提下，光谱加宽范围与脉冲半宽度τ成反比关系。

（3）加宽后的光谱分布曲线总是存在着周期性调制，调制后光谱极大值的数目，由趋近于［Δφmax/（2π）］值的正整数所决定。

上述前面两个特点，与式（6-45）所预计的结果完全一致。至于第三个特点，则可通过考察如图6-11（c）所示频率啁啾曲线而获得解释。为此，对任意一个给定的频移值而言，总是对应着两个不同时刻的脉冲成分的贡献，这样两种贡献成分之间可产生干涉效应，从而给出依赖于彼此间相差的具有极大与极小值的周期分布［26］。

最后，还应注意到的一点是，在假设的入射脉冲具有前后对称的时间波形，而介质具有瞬时折射率变化反应的前提条件下，加宽后的光谱分布亦具有相对于入射光中心频率而言左右对称的特性。但是在下述情况下加宽后的光谱分布将表现出左右不对称的特点：①入射脉冲波形前后不对称；②入射脉冲对称但是相移随时间变化曲线前后不对称。后一过程，往往发生在入射脉宽小于介质折射率变化响应（上升或下降）时间的情况下，此时相移曲线前后不对称，因而光谱加宽曲线左右（高低频）亦不再对称［27～29］。