稳态自聚焦解析理论-非线性光学与光子学成果

1）光场传播的非线性波动方程

从麦克斯韦电磁场方程组出发，可以导出电磁场在各向同性非磁性介质内传播时满足的波动方程的一般形式为

式中，μ0为真空中的磁导率。如果进一步所考虑的是准单色、准平行的强光场，则从式（5-12）以及式（5-13）可知：

式中，（ω，-ω，ω）为介质有效三阶电极化系数。将式（6-6）代入式（6-5）后可求得

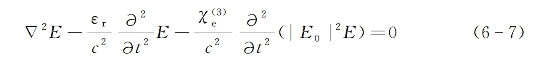
式中，c为真空中光速。如果假设0，则上式变为普通的线性波动方程。将入射波场表达式（6-1）代入以上非线性方程后可求得

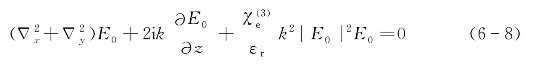
式中，k为波矢模量，而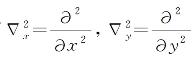。在得出上式的过程中，已经作了如下的两种假设：①入射光场的振幅函数E0为空间的慢变化函数，因此可假设其沿z轴的二阶空间导数为零；②振幅函数随时间的变化远慢于折射率响应变化的上升和下降特征时间，故E0的一阶和二阶时间导数项均可忽略（稳态假设）。为简单计，进一步假设光束振幅和波面相对于传播方向而言具圆对称性，有

式中，A（r，z）为实振幅函数，S（r，z）为表征波阵面偏离平面波程度的相位函数，r为横向径向变量，z为由入射面算起的在介质内的传输距离。将式（6-9）代入式（6-8）后可得

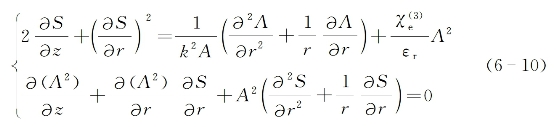
2）稳态非线性波动方程的近似解析求解［4］

当=0时，球面波（平面波是它的一种特例）是满足方程式（6-10）的一种解。因此在≠0的情况下，该方程的解仍可为球面波，只不过此时波场的横向振幅分布和波面参数随传输距离而变。为此，作如下试解：

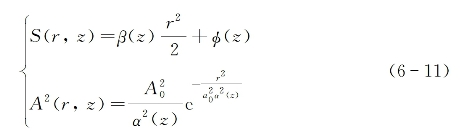
假设光束具高斯型横向光强分布，A0为初始光束中心振幅，a0为横向光强降为中心光强（1/e）倍处的特征光斑半径，而β（z）和α（z）为一待求的因子函数。入射初始条件为

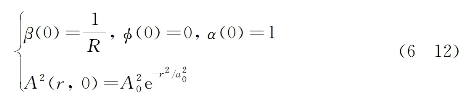
式中，R为初始波面曲率半径。

试解式（6-11）的物理含义是，对于具有高斯光强分布的球面入射波束来说，它们在能产生自聚焦作用的介质的传输过程中，仍然保持为球面波形式，但波面曲率半径通过因子β（z）随z变化，而高斯型横向光强分布的特征半径尺寸通过因子α（z）随z变化。以上这些假设，只有在近轴近似下才成立。

将式（6-11）代入式（6-10）中第一式并利用如下近轴近似

可分别求得β（z）和φ（z）满足的方程为

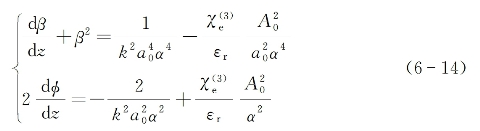
将式（6-11）代入式（6-10）中第二式后可求得α（z）满足的方程为

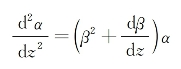
再利用式（6-14）可将上式写成只含α（z）的方程为

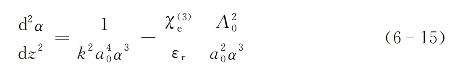
从式（6-14）和式（6-15）可以看出，一旦α（z）获得求解，则β（z）和φ（z）亦可随之解出。

将式（6-15）两端同时乘以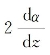，并对z进行积分后可求得

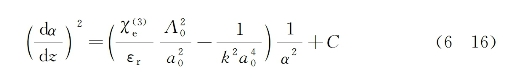
式中C为一积分常数。利用初始条件式（6-12），不难最后求得α（z）的解为

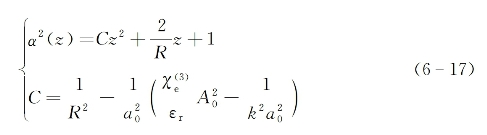(www.xing528.com)

回顾振幅函数A（r，z）的表达式（6-11），可见在非线性介质内光束的特征光斑尺寸a0α（z）随传播距离z而变，且当α（z）→0时，A2（0，z）→∞，这对应于自聚焦光束的焦点情形。在式（6-17）中令α（z）→0，可求得自入射面算起的焦点位置（焦距）为

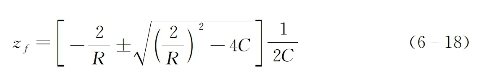
为进一步讨论方便起见，上式还可改写为

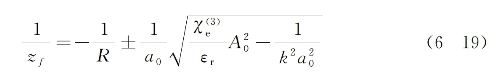
下面就几种特殊的入射波情况，对光束自焦距的行为进行讨论。

3）不同入射条件下的光束自焦距行为

（1）平面波入射。此时有R→∞而由式（6-19）表示的自焦距取正值：

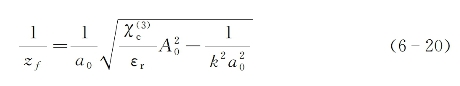
上式根号中第一项因子代表自聚焦导致的会聚作用，第二项因子表示由有限截面尺寸内所决定的衍射发散作用。当这两种作用相互平衡时有zf→∞，这意味着光束可保持不发散地在介质内传播，此时定义的入射光临界振幅条件为

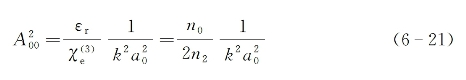
借助光强与场振幅之间的关系式（1-31），可求出光束功率P与场振幅之间的关系为

将式（6-21）代入上式后，可求出具有横向高斯光强分布的平面波入射并产生光束自陷时的临界光功率要求为

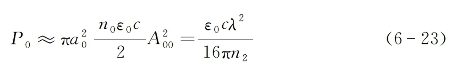
式中，λ为入射光在真空中的波长。基于以上两个公式，可将高于临界光功率入射条件下的式（6-20）简化为

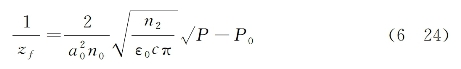
相应的自聚焦焦距为

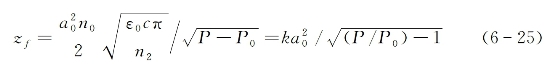
上式表明，具较高功率的入射光束可产生较短的自聚焦焦距，而在给定的入射光功率水平，光斑较小的高斯光束更容易产生自聚焦。

（2）会聚球面波入射。此时有R＜0，而式（6-19）变成为

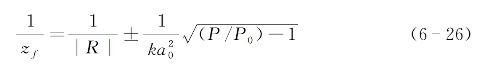
自聚焦作用的结果，是原入射光束的会聚点向入射面方向移动。当入射波为弱会聚并有时，式（6-26）右边第二项只取“+”号，此时只有一个焦点；当入射波为强会聚并有时，式（6-26）右边第二项前可取“±”号，此时除原会聚点向入射面方向前移外，还将在其后面出现第二个会聚点。

（3）发散球面波入射。此时有R＞0，而式（6-19）右边第二项只能取正值，亦即有

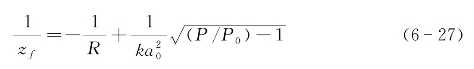
如果期望zf＞0，则要求

上式表明，在给定功率的条件下，要想使一发散的高斯光束在介质中产生自聚焦，该入射光束的发散程度不能太大。但在提高入射功率的前提下，即使有较大的入射发散程度，仍可产生自聚焦。

基于上述近似解析解所得出的几种物理结论，可直观地表示在图6-4中。其中图（a）为平行入射产生自聚焦，图（b）为弱会聚入射产生焦点前移，图（c）为强会聚入射产生双焦点，而图（d）为弱发散入射产生自聚焦的情形。

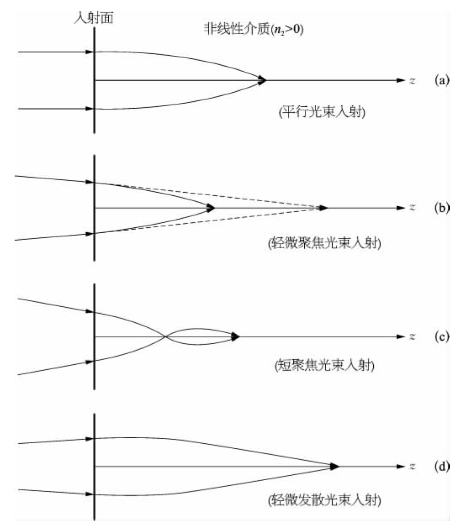
图6-4　高斯光束在不同入射条件下的自聚焦形态

（a）平行入射；（b）弱会聚入射；（c）强会聚入射；（d）弱发散入射