二阶非线性电极化导致的折射率耦合变化(光频泡克耳斯效应)

本章到目前为止所讨论的，按粗略的习惯性说法，都是由三阶非线性电极化效应导致的介质折射率感应变化；这类效应的出现，对介质种类（固体、液体、气体）和入射光场的振幅、相位等因素均无特殊要求，只要求入射光强足够高就可以了。本节将进一步表明，在二阶非线性晶体介质之中，利用三波混频效应，亦可实现介质折射率的感应变化，这种变化量的大小与参与作用光场的振幅一次方成正比；并且效应的出现，对参与耦合作用的两不同频率的作用光场的初始振幅和初始相对相位有特殊的要求。产生这种折射率变化的物理机制是纯粹电子云畸变。第13章将讨论利用这种折射率耦合变化的原理可以在二阶非线性晶体介质中形成光学空间孤子。

考虑在二阶非线性晶体内发生的一种特殊形式的三波混频过程，亦即有两束频率分别为ω和2ω的强单色相干平面光波，同时以相位匹配方式入射到介质内并产生非线性耦合作用，如图5-7所示。这种作用的结果，一方面可以导致两波能量之间的交换转移（如第3章中光学二次谐波或参量放大的情况）；另一方面，在一定的条件下，亦可引起两波场在介质内传输相位特性的变化，从而导致折射率的感应变化［21，22］。为讨论简单又不失普遍意义起见，进一步假设介质为常用的负单轴晶体，而两束入射光的偏振状态和晶体取向的安排，是以两种可能的（第Ⅰ类或第Ⅱ类）方式满足产生二次谐波的相位匹配条件。

首先考虑满足第Ⅰ类相位匹配（o，o→e）的情况。此时，按z轴方向传播的两入射平面光波分别为

图5-7　在二次非线性晶体内通过基频光与谐波光耦合而产生感应折射率变化

式中，ao和ae分别为晶体寻常光（o光）和非寻常光（e光）偏振方向上的单位矢量，k和2k分别为基波和二次谐波的波矢模量，而θ1和θ2分别为两入射光场在晶体入射面位置处的初始相位因子。这里因假设两入射光为平面波，故振幅A（ω）和A（2ω）均为实函数。在只考虑二阶非线性电极化效应的前提下，介质内频率分别为ω和2ω的电极化强度分量为

在上式基础上，可进一步写出相应频率处的电位移矢量的傅里叶分量（以ω分量为例）：

将式（5-53）代入上式后可得

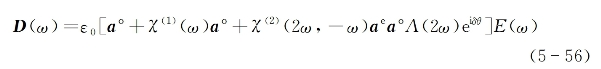
式中，相位差δθ定义为

然后以ao标乘式（5-56）等两端，则可得出矢量D（ω）在ao方向上的投影分量为

式中，εo可理解为介质在ao方向上的相对介电常数。由此可进一步求出介质对于频率为ω的寻常光所表现出的折射率为

式中，为按下面方式定义的普通弱光作用下介质对寻常光（o光）的折射率：

根据相似的推导过程，同样可写出ne（2ω）的表达式，然后可将两种频率处的折射率感应变化量一并写出：

以上表达式的物理含意是，在三波混频情况下，介质折射率的感应变化量一般表现为复数形式，其虚部决定两入射光波振幅的相对变化，而实部则表征真正的折射率变化。设晶体介质对ω和2ω光而言为透明介质，单光子与双光子共振效应可忽略，则χ（2）（2ω，-ω）和χ（2）（ω，ω）等可看成实数。将式（5-61）中含相对相位差的复指数因子按三角函数展开，然后只取其实部可得介质折射率的实际变化量为

进一步利用介质二阶非线性电极化率的运算关系：(www.xing528.com)

式中，可称为第Ⅰ类相位匹配条件下介质产生二次谐波过程的有效非线性电极化系数（为一标量）。这样，可将式（5-62）进一步简化为

既然上述折射率变化是两入射光场在介质内发生二阶非线性耦合作用的结果，因此要求在整个作用过程中折射率的相位匹配条件恒得到满足，亦即

既然开始时已假设两波场按静态相位匹配方式入射，亦即有，则动态相位匹配要求：

将式（5-64）代入上式后，可求得对两入射光振幅的要求为

即基波入射光强应为谐波光强的2倍。

由式（5-64）可看出，当时，Δno（ω）=Δne（2ω）=0，此时折射率不发生变化，这对应于普通二次谐波或光学参量放大的情况（只发生不同光波间的能量交换）。但当以下条件：

满足时，两入射光波间不发生任何能量交换，而非线性耦合的作用结果使折射率发生最大限度的变化

式（5-69）的物理含义是，在由式（5-67）和式（5-68）所表征的条件得到满足的前提下，二阶非线性晶体可发生最大限度的并与作用光场振幅成正比的感应变化，这可称为光频泡克耳斯（Pockels）效应［21，22］。当δθ=0时，折射率变化量取正值，当δθ=π时，折射率变化量取负值。

对于负单轴晶体和第Ⅱ类相位匹配（o，e→e）之情况，可设入射作用光场分别为

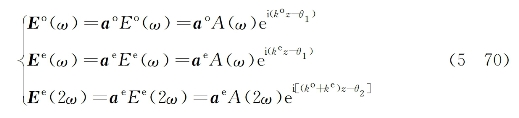
这里，假设两种偏振方向不同的基波分量具有相同的振幅函数和初始相位。则经过相类似的推导过程，并假设式（5-67）和式（5-68）所表征的条件得到满足的前提下，可最终求得与三种波场对应的最大折射率变化量为

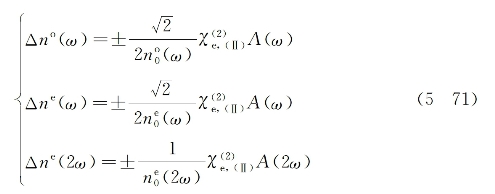
式中，

为表征第Ⅱ类相位匹配的二次谐波过程的有效非线性电极化系数（为一标量）。

本节所采用的推导光频泡克耳斯效应的分析方法，在原则上还可推广到其他的三波混频过程以及更一般的四波混频过程，用来讨论满足特殊振幅关系与初始相位条件下介质折射率的感应变化问题［21～25］。

研究光学介质在光场作用下折射率感应变化规律，具有明显的学术价值，因为利用这种变化规律可以解释一系列有关的非线性光学效应（如本书后面要讨论的自聚焦、自散焦、自调制与自加宽等）。这种折射率的感应变化，也构成了光学相位共轭、光学双稳态、非线性偏振光谱学、光学时间和空间孤子等效应的物理基础。从发展的眼光来看，介质折射率的光致可控变化，为今后的光学集成，光学逻辑线路，光学计算机，光学全息以及光学信息存储、处理与显示等技术的进一步发展，提供了重要的物理依据。这就如同20世纪40～60年代半导体物理研究的成果，为以后半导体电子学与集成技术的发展，提供了重要的物理前提一样。