分子再取向克尔效应引起的折射率变化表达式

如前所述，再取向光克尔效应主要发生在一些由各向异性分子组成的透明液体中。为简单起见，假设组成液体的分子具有两维各向异性，亦即分子有一旋转对称轴，沿该轴方向上的分子极化率为α//，而垂直于该轴方向上的分子极化率为α⊥，且有α//＞α⊥。这种假设，基本上符合最具代表性的光克尔型液体二硫化碳（CS2）。在无外光场作用时，大量分子的取向为混乱随机分布，因而液体呈现出宏观各向同性。

图5-4　入射光场矢量E，液体分子对称轴（沿x轴）以及分子感应电偶极矩矢量p之间的相对取向

如图5-4所示，假定入射光场E=a0E0为沿a0方向上的线偏振光，而所考虑的某一分子的旋转对称轴（沿x轴取向）与入射光场偏振方向之间的夹角为θ，分子的感应电偶极矩矢量为p，则该分子与光场之间的相互作用势函数为

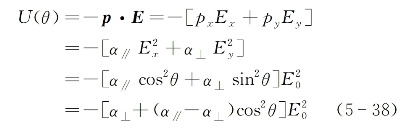
由上式可见，夹角θ值越小，相互作用势能越小，则分子在外光场中显得越稳定，这意味着组成分子液体的各向异性分子，有沿光场偏振方向上再取向的趋势，这就是所谓的光频克尔（Kerr）效应。

在稳态和热平衡条件下，分子集合相对于外加光场偏振方向上的相对分布可求出为［14］

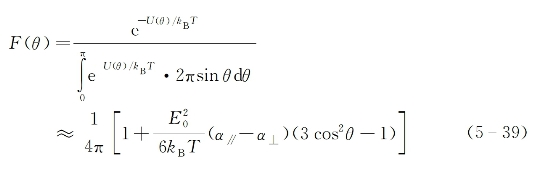
式中，kB为玻耳兹曼常数，T为绝对温度，并假定了方括号中第二项贡献远小于第一项。由上式可看出，全部液体分子相对于外加光场偏振方向而言，呈现出对称的取向分布：沿光场偏振方向上的分子取向数目最多，而沿垂直于光场偏振方向上的分子取向数目最少。这种对称取向分布的结果，是使统计合成后的介质宏观电极化强度方向仍按光场E的方向，并使液体介质呈现出感应各向异性的特点。设光场偏振方向上的单位矢量为a0，则单个分子感应电偶极矩矢量在此方向上的贡献分量为

而宏观电极化强度矢量的大小可按以下积分求得［14］

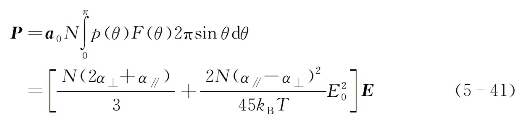(www.xing528.com)

式中，N为液体的分子密度。将以上求出的式（5-41）代入式（5-1），可得电位移矢量：

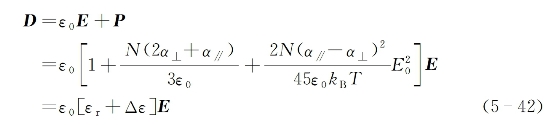
式中，εr为该液体的线性相对介电常数。而由光场引起的相对介电常数变化为

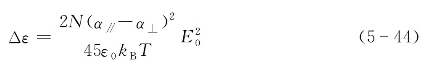
从式（5-43）与式（5-44）可看出，此时εr和Δε均为实数，因此分子再取向克尔效应是一种非共振过程。最后，可求得由入射线偏振光场导致的液体折射率变化量为

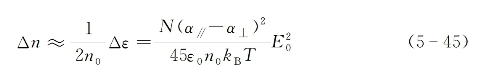
式中，n0为不加强入射光场时的介质普通折射率。将上式与前面就一般化三阶非线性电极化理论所推导出的折射率变化公式（5-15）相比较，可看出两者在形式上相同。为此，还可进一步将再取向克尔效应机制情况下的非线性折射率系数写为

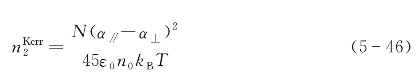
由于光频克尔效应发生在宏观各向同性的液体之中，而强光引起的折射率变化又正比于入射光强，因此习惯上人们亦把它列入三阶非线性效应之列；尽管它的产生原理同来源于电子云畸变的其他三阶非线性效应完全不同。实验表明，当入射激光的脉冲持续时间长于10-12 s量级时，在克尔型液体中产生较大折射率变化的主要贡献来自分子的再取向。