拉曼共振引起的折射率增强效果

本节讨论两束频率不同的相干光（ω1＞ω2）同时入射到拉曼介质中，通过满足拉曼共振条件而产生折射率的增强变化［2，5，7～9］。此时要求两束入射光频率之差趋近介质的某一拉曼跃迁频率（Δωr），亦即有|ω1-ω2|Δωr。在这种情况下，根据第18章中有关三阶电极化率的拉曼共振增强理论，描述介质折射率耦合变化的有效三阶电极化系数的共振增强贡献，可写为［参见式（18-93）和式（18-94）］

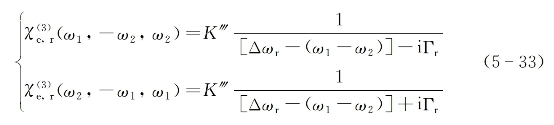
式中，Γr是所考虑的拉曼跃迁的线宽因子，K‴则是由下式定义的实数系数：

从式（5-33）可看出，拉曼共振增强的有效三阶电极化系数为一复数量，其虚数部分描述高频（ω1）光的衰减和低频（ω2）光的增益，而实数部分则描述介质折射率的耦合共振增强变化。将式（5-33）代入式（5-25）后可得

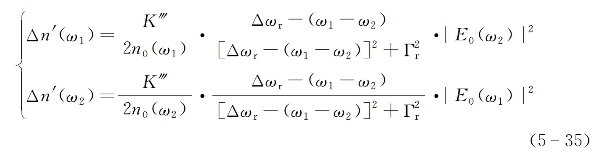
可以认为n0（ω1）≈n0（ω2）≈n0，则有简化后的表示式：

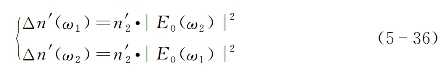(www.xing528.com)

式中

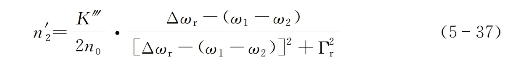
基于上式，可以绘出如图5-3所示的描述拉曼增强的折射率耦合变化的非线性系数共振调谐曲线。

图5-3　拉曼共振情况下非线性折射率系数的调谐变化曲线

由式（5-36）可看出，双光束共振耦合作用的特点，是一种入射光频率处的折射率变化，由另外一束入射光的光强所决定。在应用上，拉曼共振引起的折射率增强变化，也是实现用一束光控制另一束光的有效途径之一。