双光子共振引起的折射率增强变化-《非线性光学与光子学》简介

在上节的基础上，继续考虑当两入射光频率之和接近于介质某一双光子吸收共振频率时的情况，此时的耦合折射率变化可获得显著增强［4～6］。为证明如此，根据式（5-22）首先写出两光束的耦合折射率变化部分：

然后考察（ω1+ω2）ωto时的共振增强行为。根据第14章有关三阶电极化率的双光子共振增强理论，描述介质折射率耦合变化的有效三阶电极化系数的共振增强贡献，可写为［参见式（18-92）］

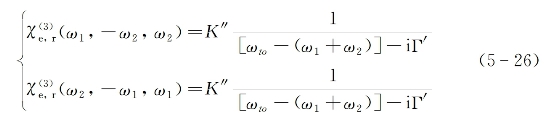
式中，Γ'是频率为ωto的双光子跃迁的线宽因子，而K"为实数常数：

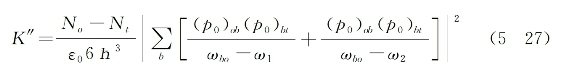
式中，No和Nt分别为分子在基态（o）和双光子激发态（t）上的粒子数密度，角标b则代表分子所有可能的其他本征能级。

从式（5-26）可看出，在满足双光子共振作用的条件下，为一复数，其虚部决定双光子吸收（截面和线形），而实部决定共振增强的折射率变化。将式（5-26）代入式（5-25）后可求得

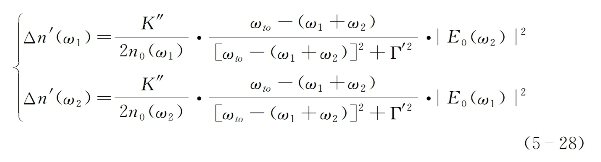
可以假设n0（ω1）≈n0（ω2）≈n0，则上式可进一步简写为

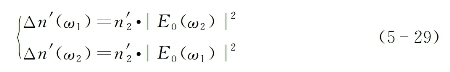(www.xing528.com)

式中，为满足双光子共振作用条件下，介质的非线性折射率系数：

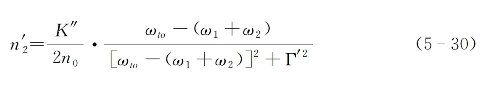
图5-2为根据式（5-30）绘出的在双光子共振频率ωto附近的调谐变化曲线。当两入射光频率之和（ω1+ω2）从较低频方向趋近于共振中心频率ωto时，折射率的共振增强变化量取正值；而当从较高频方向趋近于共振中心频率ωto时，折射率的共振增强变化量取负值；而当ωto-（ω1+ω2）=±Γ'时，折射率变化量达到极大值。这意味着通过失共振调谐，既可以控制折射率变化的正负性，又可以控制折射率变化量的大小，这些特性对某些应用来说是十分重要的。

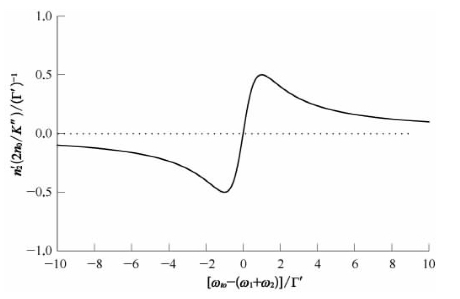
图5-2　双光子吸收共振情况下非线性折射率系数的调谐变化曲线

实际上，利用单独一束可调谐激光入射，可以更方便地实现双光子共振增强的折射率变化。此时只要求入射光频率ω满足条件2ω≈ωto，而式（5-30）可改写为

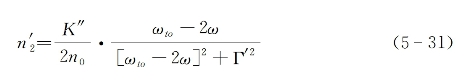
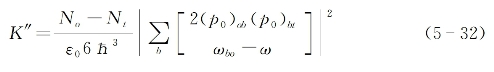
如第4章中有关四波混频共振增强的说明中所指出的那样，与单光子吸收的情况不同，双光子吸收造成的入射光衰减，只有当调谐到准确共振和光强十分高的情况下，才可能变得不可忽略。因此可以说，双光子准共振是获得折射率增强变化的最有效的方法之一。此时既可以获得较大的折射率变化，又可以实现极其快速的时间响应。