线性光学中对折射率的描述

光学介质在角频率为ω的单色光频电场矢量E的作用下，其内部电位移矢量D为

式中，ε0为真空中介电常数，P为介质内电极化强度矢量。在线性光学近似下有

式中，χ（1）（ω）为介质线性电极化率。将式（5-2）代入式（5-1）后有

式中，εr（ω）为介质的相对介电常数，它只由介质线性电极化率所决定；后者为二秩张量系数（可以为复数），但对各向同性介质而言它退化为一标量系数。

普通折射率被定义为介质相对介电常数实数部分之开方的形式，亦即

在入射光频率远离（远低于）介质任何吸收共振频率的前提下，线性电极化率为实数并可推导出为［参见第18章式（18-47）］

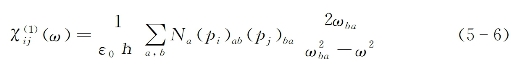
式中，为普朗克常数除2π，（pi）ab=（pi）ba为分子本征能级a与能级b之间偶极跃迁矩阵元，ωba为两能级间跃迁频率，Na是能级a上粒子密度，而角标a和b则分别代表分子所有可能的本征能级。(www.xing528.com)

对各向同性介质而言，非共振线性电极化率为一标量系数，则由式（5-5）可得

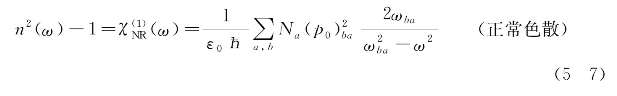
式中，（p0）ba是跃迁矩阵元，p0为电偶极矩算符矢量在入射光偏振方向上的投影。在导出上式过程中，已经假设了入射光频率ω远小于分子任何共振吸收频率ωba，故从式（5-7）中可以看出，折射率随ω的增加而变大，这对应着正常色散的情况。折射率随频率变化的正常色散行为，如图5-1中的虚曲线所示。

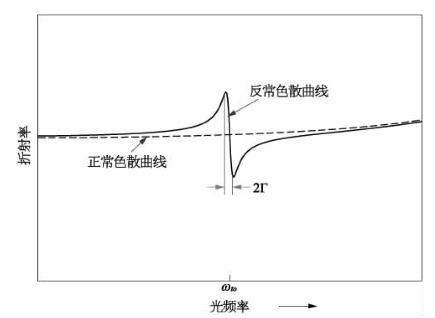
图5-1　折射率随频率变化的正常色散曲线和反常色散曲线（ωto为介质某一线性吸收频率）

现在进一步考虑当入射光频率足够靠近介质某一（单光子）吸收频率的情况。此时的线性电极化率由两部分组成：一部分是仍由式（5-7）表示的非共振贡献（为实数），另一部分是共振贡献（为复数）。后者可表为以下的复数形式［参见第18章式（18-87）］：

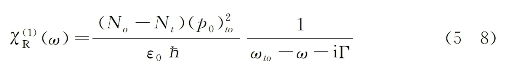
式中，ωto代表分子由基态（o）向激发态（t）产生吸收跃迁的共振频率，Γ为该跃迁的线宽因子，No和Nt分别代表低、高能级上的粒子数密度。众所周知，上式中的虚部决定了介质的线性吸收特性（截面和线形），而实部则决定了介质折射率的反常色散特性。将式（5-8）中的实数部分代入式（5-5）后可求得

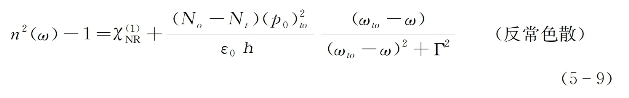
根据以上公式，反常色散曲线如图5-1中实线所示。

从本节的说明可以看出，在线性光学范围内，在共振与非共振两种情况下，介质折射率均与入射光强无关。这一结论，为激光出现以前的众多实验所证实。