光纤中二次谐波的产生：非线性光学与光子学

在非线性光学的早期研究中，人们曾认为在光纤样品中会很难产生二次谐波，因为它们的芯材料为各向同性的玻璃。然而，从1980年代起，人们开始在长度为几十到几百米的单模或多模光纤中观察到弱的SHG信号［65，66］。稍后，一个欧洲的研究小组进一步在长度很短（0.5～1 m）的掺Ge和掺P的单模光纤样品中观察到很强的SHG信号［67，68］。但在后一种情况下，需要用1.06 μm的基频激光经光纤端面输入，对样品进行长达几小时辐照后，输出SHG信号可达到较高的水平，转换效率可≥5%。这一结果引起了研究者们的兴趣。之后，美国电话电报公司的研究小组报道了利用短光纤样品实现SHG的另外一种实验安排，并进而对所观察到的效应，给出了一种物理解释［69，70］。

按照上述第二种实验安排，被测光纤样品首先被1.06 μm基波光束和532 nm谐波光束同时入射辐照；经过一定时间后，入射谐波辐照被解除，然后相当强的二次谐波发射可在光纤输出端一直观测到。该情况下所需要的辐照时间，取决于两入射光束的强度水平，可为几分钟到几小时，而最终的转换效率可达0.24%。

基于该实验提出的理论模型［69，70］，后面观测到的谐波输出是来自两个相继的非线性过程。第一个过程是由ω基波与2ω谐波通过三阶光学混频（整流）效应而产生感应的空间周期变化的直流场，其对应的三阶非线性极化强度（忽略其矢量性质）为

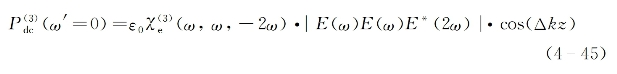
式中，Δk=2k（ω）-k（2ω）为相位失匹配因子，z为光纤内的传播距离。该过程导致了光纤芯内沿传播方向上周期为2π/Δk的直流场空间变化。从另一方面考虑，在被掺杂过的光纤芯材料内，存在着由静电场或入射激光诱导的色心、缺陷或俘获中心等，它们可以在激光感应直流场作用下通过电荷分离或本身的再取向而引起对中心对称性的局部偏离，从而提供了产生SHG的可能性。后者的产生可由以下的二阶非线性电极化（忽略其矢量特性）来描述：(www.xing528.com)

可进一步假设这里的有效二阶非线性极化率系数（ω，ω）的大小与空间分布，是决定于由式（4-45）表示的感应直流电场。这也意味着大小随空间的变化周期π/Δk恰好等于在Δk≠0情况下产生二次谐波时的有效作用长度l0［参见式（3-11）和图3-2］，因此SHG信号可在光纤内远大于l0的传输距离上不断得到增长。

另一种可能性是，既然存在着由式（4-45）所表述的感应直流场，则通过dc场参与的三阶混频效应，亦可产生有效的SHG输出。

以上介绍的物理模型，也可以用来解释采用单独一束基频光入射到光纤样品的实验结果［67，68］。此情况下，可假设光纤内的初始微弱SHG信号是借助于磁偶极与电四极贡献而产生，或者由于局部中心对称性偏离而产生。这样产生的弱SHG波与强基波相互作用而感应出上述的直流场，从而促成SHG波的进一步增强。