相干与反相干环状辐射的产生

前面讨论了在四波混频过程中，由双光子和频共振导致的增强作用，亦即入射光中两个光子频率之和（2ω或ω1+ω2），趋近于介质某一双光子吸收跃迁中心频率（ω0）时的情况。本节将考虑另外一种类型的共振增强，亦即入射光中两种光子频率之差（ω1-ω2），趋近于介质某一拉曼跃迁频移值（Δωr）时的情况。此时，如图4-7（a）所示，假设有两种频率分别为ω1和ω2的单色相干光同时按同一方向入射，且有ω1＞ω2以及ω1-ω2≈Δωr条件成立，则这一过程可称为拉曼共振增强的四波混频或四光子参量作用。该过程的实质，仍可表述为频率为ω1和ω2的两个入射光子的湮灭以及频率为ω3和ω4的两个新光子的同时产生，只不过由于拉曼共振作用，过程发生的概率显著得到增强。按能量守恒要求，参与作用的4个光子的频率应满足如下关系：

而动量守恒则要求如下的波矢匹配条件：

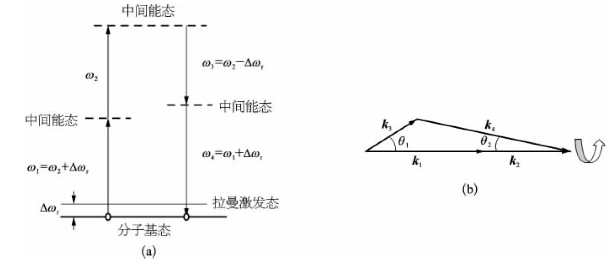
图4-7　拉曼共振增强四波混频的跃迁图解（a）及非共线波矢匹配（b）

在假设k1和k2为同向入射前提下，如图4-7（b）所示，k3和k4取向一般必须与入射光有所不同；亦即新产生的两种频率不同的光子按偏离入射方向不同的角度上传播。这两束新产生光传播角度之具体大小，由介质拉曼频移值和它的折射率色散所确定。对液态和固态介质而言，θ1和θ2的取值范围在1°～4°之间。在图4-7（b）中，如果以入射方向为轴将波矢匹配三角形旋转360°，则该匹配条件恒得到满足。因此我们可期望两种圆锥状相干光束的产生，其中频率为ω3=ω2-Δωr的光称为相干斯托克斯辐射，而频率为ω4=ω2+Δωr的光称为相干反斯托克斯辐射。

需要特别指出的是，在整个上述过程之中，并未涉及任何分子的实际拉曼跃迁（基态至拉曼振动激发态），因此这种过程从本质上来说，不同于普通拉曼散射或受激拉曼散射。

与相干斯托克斯和反斯托克斯辐射对应的介质三阶电极化强度分量为

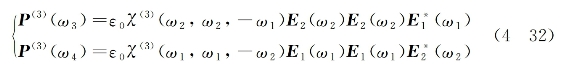
与式（4-20）的推导相类似，在相位匹配满足的条件下，两新产生光束输出光强为(www.xing528.com)

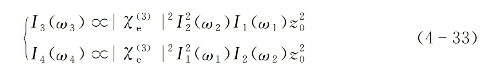
式中，（ω2，ω2，-ω1）=（ω1，ω1，-ω2）是按类似于式（4-13）方式定义的有效三阶非线性电极化系数，z0为介质的有效作用长度。基于第18章有关三阶非线性电极化率的详尽理论，在满足下面拉曼共振作用的条件下

描述四波混频过程的有效三阶电极化系数共振增强部分的贡献为

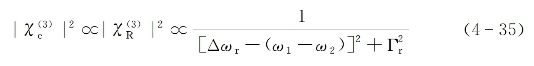
式中，Γr为介质拉曼跃迁的线宽因子。从上式可以看出，当ω1-ω2Δωr时，过程的发生效率可显著增强。

图4-8为观察拉曼共振增强四波混频的实验装置示意图。频率为ω1和ω2的两束激光同方向入射到一拉曼介质，其中一束光为可调谐；则当这两束光之频率差足够接近介质拉曼共振频率时，可在放置于介质后面的一个观察屏上，看到两个颜色不同的窄光环。如果能进而记录它们的信号光强作为两入射光频差之函数，则可用这种方法研究介质的拉曼光谱特性。

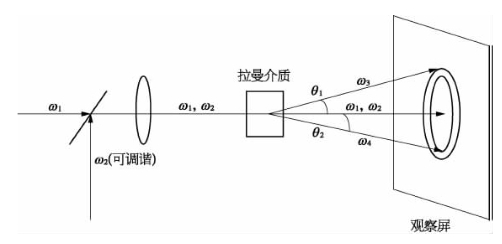
图4-8　观察拉曼共振增强四波混频的实验装置示意图

这里分析的拉曼共振增强四波混频原理，有助于解释第7章将要介绍的有关受激拉曼散射实验中有时出现的环状相干辐射的现象［46～52］。在那一类实验中，频率为ωp的泵浦光首先产生方向相同但频率为ωp-Δωr的斯托克斯受激拉曼散射光；然后这两种满足拉曼共振条件的光相互作用，按本节所述原理进一步产生频率分别为ωp+Δωr和ωp-2Δωr的环状辐射。前一受激拉曼散射过程不要求相位匹配条件，而后一过程为四波混频（四光子参量）过程，故要求相位匹配。