三次谐波相位匹配的实现方法非线性光学与光子学

从本章到目前为止的说明中可以看出，满足相位匹配是实现有效三次谐波和其他四波混频效应的最为关键的要求。为满足这一要求，可根据实验条件和非线性介质的不同，而采取不同的方法和措施。以下只列举三种可行的例子。

（1）双折射补偿。在各向异性的晶体介质中，可利用折射率的双折射效应来补偿色散效应。以负单轴晶体为例，产生共线作用三次谐波的折射率匹配可分别按下述三种可能的方式实现：

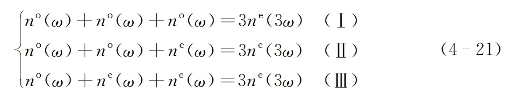
（2）混合介质中的色散补偿。假设所使用的非线性介质（气体或液体）由两部分组成：具有折射率正常色散的组分a，以及具有反常色散特性的组分b。对前者有na（ω）＜na（3ω），而对后者有nb（ω）＞nb（3ω）。则适当调节两组分的相对比例，可使相位匹配按下面的方式实现：

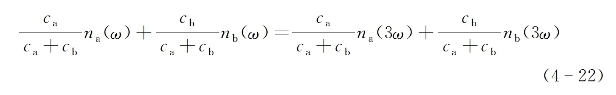
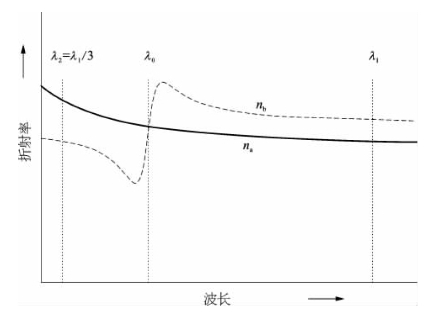
式中，ca和cb分别为两种成分的克分子浓度。如图4-2所示：图中na随波长变化由一条实曲线表示，而nb由一条虚曲线表示。对组分b材料来说，在λ0波长位置处有单光子共振吸收，故在其两侧一定光谱范围内出现折射率的反常色散行为。在适当相对克分子浓度比例的前提下，有可能在基波波长λ1与三次谐波波长λ2=λ1/3之间实现折射率相等的匹配要求。

(www.xing528.com)

图4-2　混合介质中两组分折射率随波长的不同变化行为

（3）通过强光引起的折射率变化实现匹配。第5章将专门介绍由强光入射在介质中引起的折射率感应变化。对各向同性的介质而言，由三阶非线性电极化效应引起的折射率变化，简单地与入射光强成正比。设所考虑的三阶非线性介质具正常色散行为，则有n（3ω）-n（ω）=Δn＞0。又进一步假设该介质为自聚焦型介质，因此由强基波入射引起的正折射率变化为

式中，n2＞0为介质的非线性折射率系数，E（ω）为基波场强。则在适当的基波入射光强水平下，有可能按以下方式实现三次谐波产生的相位匹配：

从实验的角度来说，上面介绍的第一种方法，只适用于各向异性晶体；第二种方法主要适用于气体和液体；第三种方法适用于具有强自聚焦特性的介质（可分别为气体、液体或固体）。