三次谐波效应的非线性电极化理论揭示了非线性光学

在非线性光学发展的早期，就已在方解石晶体（具对称中心）、NaCl、KCl等立方晶体以及光学玻璃等固体介质中成功地观察到光学三次谐波效应，但由于相位匹配条件得不到满足，因此谐波转换效率是十分低的［1］。

与三次谐波产生相对应的三阶非线性电极化强度分量为

式中，E1（ω）是入射基频光的电场强度，χ（3）（ω，ω，ω）是表征三次谐波产生的介质三阶电极化率。进一步将基频场和三次谐波场写成如下单色平面线偏振波形式：

则对应的三阶非线性电极化强度分量表示式为

将式（4-9）代入式（4-10）后得

为求解两种波振幅函数沿同一传输方向上的变化，将式（4-11）第二式代入耦合波方程式（2-47）可得

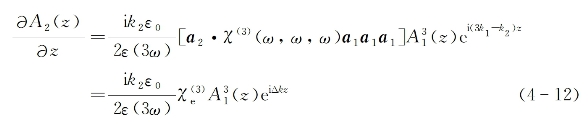
式中，

是表征给定介质产生三次谐波的有效三阶电极化系数，而

则是失相位匹配因子，它正比于介质在基频和三倍频处折射率之差。(www.xing528.com)

首先分析相位不匹配（Δk=3k1-k2≠0）的情况。此时，由式（4-9）和式（4-11）中第二式的比较中可看出，P（3）（3ω，z）波和E2（3ω，z）波的相速度不同，因此基波能量不能有效地转移到三次谐波辐射之中。在这种情况下基波振幅沿z轴变化可近似忽略，从而有

则式（4-12）的解为

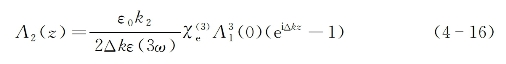
而三次谐波光强可表示为

式中，I1（0）∝|A1（0）|2是入射基波光强。式（4-17）与相位不匹配情况下导出的二次谐波光强公式（3-10）相似，并同样可由图3-2中曲线来表征。此时，三次谐波光强沿z轴呈周期性变化，变化周期为2π/Δk，而其值之一半定义为三次谐波产生的相干作用长度：

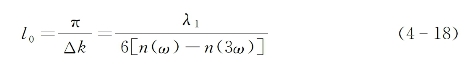
由上面的分析可见，较小的失相位匹配Δk值，提供较高的峰值谐波光强和较长的相干作用长度。为显著提供三次谐波产生的效率，必须做到Δk0或n（ω）n（3ω）。对大多数透明单纯光学介质，正常色散决定了n（3ω）＞n（ω），但采用后面将要介绍的一些特殊方法，仍有可能实现三次谐波产生的相位匹配。考虑到与二阶电极化效应相比，三阶电极化效应更为微弱，因此即使在实现相位匹配的实验条件下，由基波向三次谐波的能量转换效率仍低于10-1量级。这意味着即使在相位匹配条件基本得到满足的情况下，前面所作基波振幅沿z轴变化可近似忽略的假设仍然成立。此时可进一步认为非线性介质与入射基波的有效作用长度（z0）远小于产生三次谐波产生的相干长度l0，亦即有

从而由式（4-17）求出在相位匹配条件基本满足的条件下，三次谐波输出光强为

三次谐波输出光强与介质产生三次谐波的有效三阶电极化系数的平方成正比，与入射基波光强立方成正比，然后与有效作用长度（介质有效厚度）的平方成正比。实际上，为获得足够高的入射基波光强，通常采用聚焦入射的方式，此时的有效作用长度z0基本由聚焦入射光束之焦深范围决定。然而，在基波聚焦入射情况下描述三次谐波产生过程的数学公式，则远比上面在诸多简化条件下得到的公式［式（4-20）］要复杂得多［2］。

对普通透明光学介质而言，产生三次谐波的有效三阶电极化系数的数值是很小的，但在采用后面将要介绍的适当的共振增强措施后，该数值可显著获得增大。