四波混频的几种方式与非线性光学与光子学

第2章着重讨论了由二阶非线性电极化过程所决定的二次谐波和一般情况下的三波混频效应。这些效应，在一般的意义上来说，只能在不具对称中心的数目有限的压电晶体中有效产生。本节将进一步讨论由三阶非线性电极化过程所决定的三次谐波和一般情况下的四波混频效应。这些效应，可在所有各种类型、各种状态的介质中产生，因此，对这些效应开展的各项研究，具有更为普遍的意义。

根据式（2-29），可以大致估算二阶和三阶非线性效应出现的相对难易程度。为此，假设介质仍为不具对称中心的晶体，入射单色激光电场强度的数值为|E|，则二阶与三阶非线性电极化强度分量的相对比值约为|E|/|E0|，这里|E0|为分子内外层电子经受的内部场强数值。在一般非短聚焦入射的情况下，入射光波的场强数值仍然在量级上显著低于介质分子内的平均场强数值。因此三阶非线性效应与二阶非线性效应相比，更加难以出现。当然，对于各向同性光学介质而言，由于在电偶极矩作用近似下二阶非线性过程是禁戒的，因此一般能观察到的大多是三阶非线性效应。

采用全量子理论的观点，同样可对三次谐波和一般情况下的四波混频过程的实质给出简明而又严格的物理描述。在这种理论框架内，四波混频基元过程的实质，涉及参与作用的4个光子之间的参量相互作用，因此亦可把四波混频过程称为四光子参量作用过程。“参量作用”是指从混频过程的始末来看，不发生光场与介质间的任何能量和动量交换。从这种意义上来说，也可以把三波混频过程称为三光子参量相互作用过程。

图4-1给出了几种典型四波混频（四光子参量）过程的量子跃迁图解。对这些示意图的物理含义的详尽解释，可参照图3-1、图3-6和图3-8等所给出的说明。

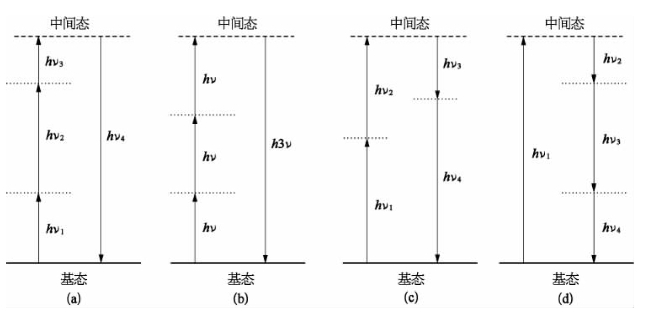
图4-1　几种典型四波混频（四光子参量）过程的量子跃迁图解

（a）三阶和频；（b）三次谐波；（c），（d）四光子参量作用

图4-1（a）为描述光学三阶和频基元过程的量子跃迁图解。为简洁起见，也可以把这一基元过程的实质，概括为在过程的第一步，涉及三个能量不同的入射光子的湮灭，而介质的分子离开初始态而跃迁至由虚能级表示的某一中间态；在过程的第二步，介质分子立刻回到初始能态并同时发射出一个和频光子。考虑到在这一基元过程之始末，参与作用的分子本身之能量与动量未发生变化，故能量与动量守恒只要求在参与作用的4个光子之间满足。

式中ki为第i种波的波矢。若假设4种光场沿同方向传播，则上面第二式表示的波矢匹配条件直接导致以下的折射率匹配条件：

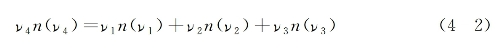
三阶和频是实现激光频率上转换的有效途径之一。如果其中一束光频率为可调谐，则和频输出光亦为可调谐。为实验方便，亦可采用只有两束光入射，在满足相位匹配条件下，其中一束起两种波作用（v1=v2），而输出和频光频率为（2v1+v3）。

若只有一束频率为v和波矢为k的强相干光束入射到介质中，则在原则上可产生如图4-1（b）所示的光学三次谐波（THG）。此情况下的能量与动量守恒要求为(www.xing528.com)

式中，v'和k'为输出三次谐波光的频率和波矢。在共线作用下，波矢匹配条件导致以下的折射率匹配条件：

很显然，由于介质的折射率色散效应，上面的要求在一般情况下，不能自动得到满足，而必须采用一些特殊的方法（见4.2节说明）。

图4-1（c）所示的是一种很基本的四光子参量作用过程，它涉及两个入射光子的湮灭和两个新出射光子的同时产生。这种情况下的能量与动量守恒要求为

图4-1（d）所示的是一种三阶和频过程之逆过程，它涉及一个高频入射光子的湮灭和三个低频光子的同时产生。此时的能量与动量守恒要求为

应该注意的是，在图4-1（c），（d）中，即使入射光的频率v1和v2（或者v1）为给定，并且相位匹配条件式（4-5）或式（4-6）得到满足的前提下，新产生的两种（或三种）光子的各自频率数值，仍然可能有一定的任意性。

到目前为止，实际上一直假设非线性介质为无吸收的透明介质，能量与动量守恒只要求在参与作用的4种光场之间得到满足。因此能量守恒要求入射光光强（之和）的减少，应等于新产生光光强（之和）的增加；而与此同时，入射光场光子数（之和）的减少，应等于新产生光场光子数（之和）的增加。以图4-1（c）所示的四光子参量作用过程为例，基于以上考虑，可以得出以下的有关光强（Ii）和光子流密度（Ii/hvi）沿传播方向上的变化方程：

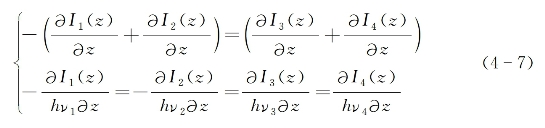
式（4-7）实际上是推广到三阶非线性混频过程的门罗（Manley-Rowe）关系式。