非线性光学与光子学的光学和频效应

本节考虑的仅仅是二阶非线性电极化过程范围内的三波混频效应，亦即两种频率不同的单色相干光波入射，在二阶非线性晶体内产生第三种频率（和频或者差频）单色相干辐射的过程［12］。

首先用全量子理论的观点来说明光学和频过程的基本物理图像，它与二次谐波过程在本质上是相同的。如图3-6所示，首先可想象在基元过程的第一阶段，在一个频率为v1的入射光子湮灭的同时，介质的一个分子离开基态能级而与光场共处于一种中间能态；在第二阶段，另一个频率为v2的入射光子湮灭而已被激发的分子跃迁到另一中间能态；在第三阶段，该激发分子重新跃迁回到其初始能级并同时发射出一个和频（v3）光子。由于分子在各中间能态的停留时间近似为无穷小，因此上述三个阶段实际上是同时完成的。

图3-6　光学和频效应的量子跃迁过程图解

由于在整个基元过程的初始和终止，介质分子的能量与动量状态并未改变，因此能量与动量守恒只要求在三个作用光子之间满足，从而下述条件成立：

式中，k1，k2和k3为三种光场的波矢，假若三种平面单色光波均沿同一传输方向在介质内传输，则波矢匹配条件导致以下的折射率匹配条件：

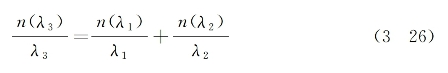
式中，λ1，λ2和λ3为三种波在真空中的波长。由于晶体折射率存在色散效应，一般情况下上述匹配条件不能自动得到满足。为此，可利用介质折射率的双折射或它的温度效应来补偿色散效应，以实现相位匹配。(www.xing528.com)

由以上的说明可以看出，二次谐波过程实质上是二阶和频过程的一种特例，亦即两入射光场具有相同频率而产生和频辐射的情况。

借助于第2章中有关二阶非线性电极化强度分量表示式和耦合波方程，可对和频过程进行定量的分析和计算。此情况下，可将参与作用的三种光场描述为

而与它们对应的二阶非线性电极化强度分量为

将以上两式代入耦合波方程式（2-47），可得到三个联立的方程组，从而可对它们进行准确或近似求解。为使和频过程有效产生，P（2）（ω3，z）波和E（ω3，z）波的相速度必须相同，因此要求以下相位匹配条件得到满足：

这一要求，与由全量子理论考虑所得出的要求完全一致。