进位计数制相互转换及单片机原理与接口技术的设计与实训

1 进制数互相转换

十进制数转换为二、十六进制数：任一十进制数N转换成q进制数，先将整数部分与小数部分分为两部分，并分别进行转换，然后再用小数点将这两部分连接起来，如图1-31所示。

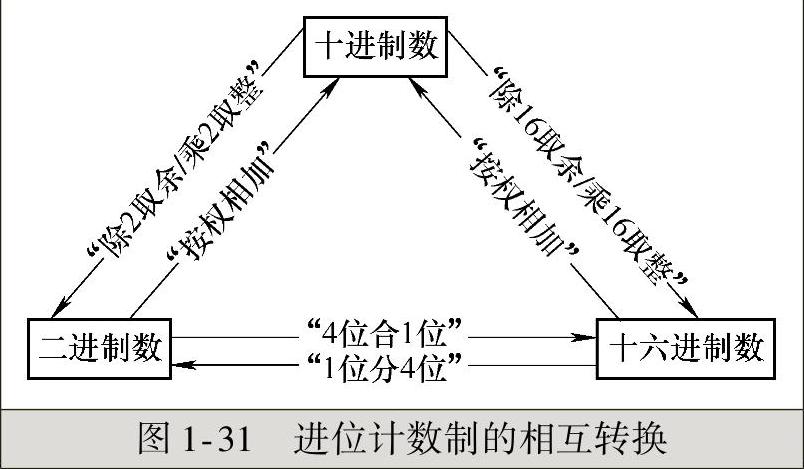
图1-31 进位计数制的相互转换

整数部分转换步骤为：第1步，用q去除N的整数部分，得到商和余数，记余数为q进制整数的最低位数码K₀；第2步，用q去除得到的商，求出新的商和余数，余数又作为q进制整数的次低位数码K₁；第3步，用q去除得到的新商，再求出相应的商和余数，余数作为q进制整数的下一位数码K_i；第4步，重复第3步，直至商为零，整数转换结束。此时，余数作为转换后q进制整数的最高位数码K_n-1。

小数部分转换步骤为：第1步，用q去乘N的纯小数部分，记下乘积的整数部分，作为q进制小数的第1个数码K_-1；第2步，用q去乘上次积的纯小数部分，得到新乘积的整数部分，记为q进制小数的次位数码K_-2；第3步，重复第2步，直至乘积的小数部分为0，或者达到所需要的精度位数为止。此时，乘积的整数位作为q进制小数位的数码K_-m。

从以上例子可以看出，二进制表示的数越精确，所需的数位就越多，这样，不利于书写和记忆，而且容易出错。另外，若用同样数位表示数，则八、十六进制数所表示数的精度较高。所以在汇编语言编程中常用八进制或十六进制数作为二进制数的缩码来书写和记忆二进制数，便于人机信息交换。在MCS-51系列单片机编程中，通常采用十六进制数。

又如，将（0.686）10转换成二、八、十六进制数（用小数点后5位表示）。

0.686×2=1.372 K_-1=1 0.686×8=5.488 K_-1=5 0.686×16=10.976 K_-1=A

0.372×2=0.744 K_-2=0 0.488×8=3.904 K_-2=3 0.976×16=15.616 K_-2=F(www.xing528.com)

0.744×2=1.488 K_-3=1 0.904×8=7.232 K_-3=7 0.616×16=9.856 K_-3=9

0.488×2=0.976 K_-4=0 0.232×8=1.856 K_-4=1 0.856×16=13.696 K_-4=D

0.976×2=1.952 K_-5=1 0.856×8=6.848 K_-5=6 0.696×16=11.136 K_-5=B

（0.686）10≈（0.10101）2≈（0.53716）8≈（0.AF9DB）16

可借助计算器将进制数进行互相转换，其界面如图1-32所示。计算器可进行多个常用进制之间的互相转换，同时将结果输出，这对于单片机进行数制转换提供了简便的方法。

图1-32 进制计算器

2 进制数的算术运算

二进制数只有0和1两个数字，其算术运算较为简单，加、减法遵循“逢二进一”、“借一当二”的原则。

二进制数除法是二进制数乘法的逆运算，在没有除法指令的微型计算机中，常采用比较、相减、余数左移相结合的方法进行编程来实现除法运算。由于MCS-51系列单片机指令系统中包含有加、减、乘、除指令，因此给用户编程带来了许多方便，同时也提高了机器的运算效率。