水利工程建设进度控制：完工概率分析

上文“二”中计算出了计划中各节点的时间参数并确定出了期望关键线路。但是，这些结果对如图4-2 所示的进度计划并未给出一个直接的定量评价。为此，下面引入完工概率这一评价标准，以衡量计划按期完工的可能性的大小。

根据概率论中的“中心极限定理”，凡是许多微小的相互独立的随机变量所组成的随机变量，认为服从正态分布。在计划评审技术中，节点的最早时间（或最迟时间）是由其前面（或后续）一系列工作的完成历时，这些独立的随机变量组成的。当这些工作充分多时，用正态分布估计节点时间是可行的。因为我们在计划中最关心的，正是那些深入网络内部接近工程结束的节点和终点能否按期完成的概率。

设工程（或某节点）在规定工期Ts前完工的概率为P（t ≤Ts），且为一正态分布函数；Te[或TE（i）]为该工程（或节点）计算的期望完成时间值，σT为标准离差。当限定了工期Ts，以后，图中曲线下面的阴影部分的面积就是该计划能在Ts前完工的概率。即：

显然，若Ts＝Te[或Te（i）]时，其完工概率P ＝0.5；当Ts＞Te时，P ＞0.5；若Ts＜Te，则P ＜0.5。此外，σT值越大，则曲线离散程度也越大。所以工程 （或节点）的完工概率P 值，主要取决于Ts、Te[或Te（i）]及σT值的大小。

例如，在工程完工概率分布曲线 （见图4-4）中，已知Te＝20 个月，σT＝3 个月。若规定工期Ts＝23 个月，则完工概率可根据式

计算出P ＝0.84，如图中曲线下阴影部分面积所示。

因此，只要知道了Te、σT及规定工期Ts，即可计算出系数λ：

(www.xing528.com)

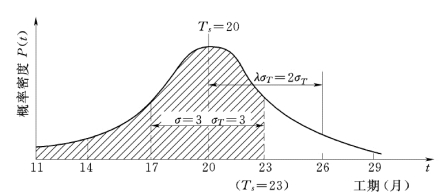
图4-4　完工概率分布曲线

根据λ值，就可以从标准正态分布表中 （λ对应表中的Z 值）查得在规定工期Ts下的完工概率P。λ称为难度系数，λ越大，表明按规定工期完工的可能性越大。

在图4-2 所示的网络进度计划中，计划完工日期Ts＝100d，该进度计划完工期的统计参数为：Te＝92 天，VT＝68.42，那么

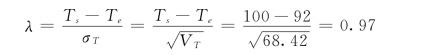
查附录2 标准正态分布表知：在规定工期Ts＝100d 条件下，[例4-1]的网络计划的完工概率为P ＝83.4%。

完工概率随计划完工期的缩短而减小，随计划完工期的延长而增大。若对图4-2 所示计划规定不同的完工期，则完工概率也不同，计算结果如表4-2 所示。

表4-2　计算结果

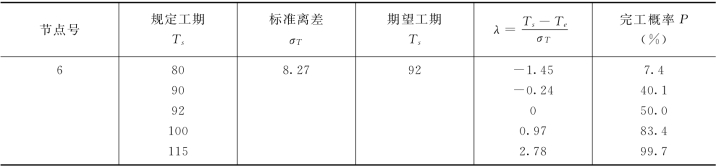
图4-2 所示计划各节点的完工概率如表4-3 所示。