节点时间参数计算，水利工程建设进度控制

由于各工作的历时是随机的，那么各节点的时间参数也是随机的。本节主要介绍节点的最早时间计算、节点的最迟时间计算、节点松弛时间或称节点时差计算以及确定网络计划的期望关键线路。

在计划评审技术中，节点时间参数计算的方法与关键线路法中节点时间参数计算的方法类似，现通过[例4-1]说明如下。

【例4-1】 某工程的网络进度计划如图4-2 所示。在对计划中影响各项工作持续时间的不确定性因素分析基础上，得出各项工作的乐观估计时间、悲观估计时间和最可能估计时间如表4-1 所示。根据式 （4-1）、式 （4-2）、式 （4-3）已将各工作的te、σt、Vt计算出，填入表4-1 中，要求计算各节点的时间参数并确定期望关键线路 （计算结果标注在图4-3 中）。

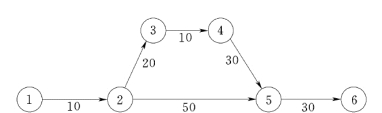
图4-2　网络进度计划图 （[例4-1]图）

表4-1　工作历时表（[例4-1]表）

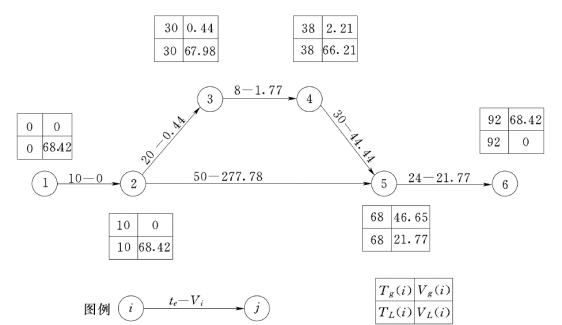
图4-3　网络进度计划评审计算示意图 （[例4-1]图）

（一） 节点最早时间期望值的计算

节点最早时间期望值的计算公式为：

式中：TE（i）、TE（j）为—节点的最早时间期望值；te（i，j）为i、j 工作的期望历时。

根据下述概率统计定量，即：

“若干相互独立随机变量的和方差等于各该随机变量本身方差的和”，可求得节点最早时间的相应方差为：

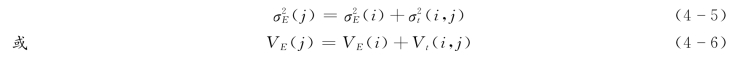
式中：σE（i）、σE（j）为、节点最早时间的均方差，节点与式 （4-4）取最大后确定的节点相同；σt（i，j）为i—j 工作的历时的均方差；VE（i）、VE（j）为—节点最早时间的方差值；Vt（i，j）为i—j 工作的持续时间的方差值。

节点最早时间期望值的计算过程为：由起点节点开始，由前向后逐节点顺推计算，直到终点节点。

起点节点的最早时间就是工程的开工时间，应是肯定的，其方差为零。本例中：

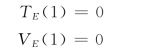
其他节点的最早时间计算，可根据式 （4-4）、式 （4-5）从前向后依次进行。

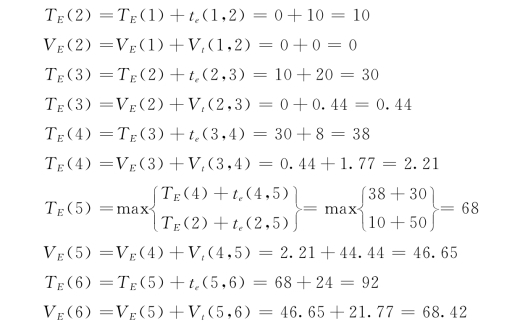
（二） 节点最迟时间期望值的计算

节点最迟时间期望值的计算公式为：(www.xing528.com)

式中：TL（i）、TL（j）为、节点的最迟时间的期望值。

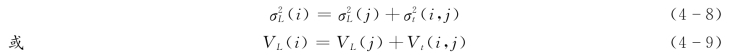
与节点的最早时间类似，节点最迟时间的相应方差计算公式为：式中：σL（i）、σL（j）为、节点的最迟时间的均方差；为节点与式 （4-7）取最小后确定的节点相同；VL（i）、VL（j）为、节点的最迟时间的方差值。

节点最迟时间的计算过程为：由终点节点起，从后往前逐节点逆推计算。

终点节点的最迟时间应等于工程计划的规定完工工期，为肯定值，其方差为零。在无特殊规定时，令终点节点的最迟时间等于其最早时间进行参数计算。本例中：

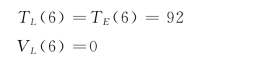
其他节点最迟时间期望值的计算可根据式 （4-7）、式 （4-9）依次在图上直接标记进行，结果如图4-2 所示。其过程为：

（三） 节点的时差计算

计划评审技术的分析及计算均以节点为基础。节点在时间上的允许变动范围称为节点的时差 （又称松弛时间），用SL（i）表示，为节点代号。

节点的时差SL（i）等于节点i 的最迟时间TL（i）与其最早时间TE（i）之差，即：

节点时差也是随机变量，SL（i）为其期望值，SL（i）值的可靠性由其方差确定，计算公式为：

或

本例中，

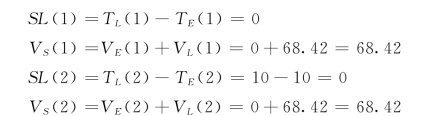
其他节点的节点时差可根据式 （4-10）、式 （4-12）依次计算。

（四） 期望关键线路

通过 [例4-1]可看出，在计划评审技术中，各条线路中有一条线路，其上各工作的期望历时之和最大，这条线路称为期望关键线路。若存在几条最长的线路，则方差大的线路为期望关键线路。本例中①—②—③—④—⑤—⑥为期望关键线路。在期望关键线路上，各节点的最早时间TE（i）与其最迟时间TL（i）相等，节点时差SL（i）也都为零。

计划的终点节点的最早时间就是工程计划的期望工期。本例中，期望工期Te＝TE（6）＝92，相应方差VT＝VE（6）＝68.42。