计划评审技术是以数量统计为基础的,因此,对于工作持续时间不确定的工作,应首先研究其持续时间的概率分布。如果在过去实践的基础上,掌握了类似工作完成时间的大量资料,即可应用统计检验的方法,确定该工作持续时间的分布规律,同时计算出各种统计参数。但是,由于建设项目的单件性,很难得到代表性好、一致性好的历史统计资料,一般多采用三点估计法进行工作历时的估计。
所谓工作历时的三点估计法,就是在项目已有的勘察、观测、试验资料基础上,参照过去实践经验,客观地估计出下列三种情况下的可能完成的时间,即 (见图4-1):
(1)乐观估计时间(Optimistic Time)。即在顺利条件下,完成某项工作所需的时间,用t0表示。
(2)悲观估计时间(Pessimistic Time)。即在最不利的条件下,完成某项工作所需的时间,用tp表示。
(3)最可能估计时间 (Most Probable Time)。即在正常条件下,完成某项工作所需的时间,用tm表示。
假定各工作的历时服从三参数β分布,则其期望值te、标准离差σt、方差Vt都可按式 (4-1)~式 (4-3)近似计算。
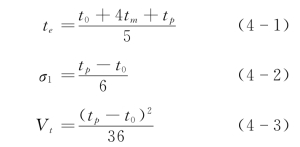
在进行了大量的随机实验后,表明工作持续时间在大多数情况下是服从β分布的。况且最乐观时间t0、最可能时间tm和最悲观时间tp也存在估计误差,而且往往这种估计误差比上述统计计算误差大得多。人们通常应把重点放在提高三个估计值的精度上。(https://www.xing528.com)
数学家华罗庚曾对式(4-1)、式 (4-2)作过很通俗的解释。假定工作时间等于tm的可能性是t0的可能性的2 倍,也是tp的可能性的2 倍,则 (t0、tm)之间的平均值是(t0+2tm)/3,在 (tm,tp)之间的平均值是(tp+2tm)/3,两者平均,得:
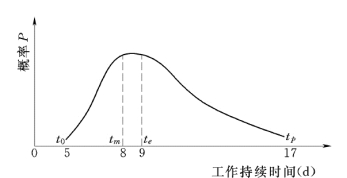
图4-1 概率分布密度曲线
![]()
这个平均值就是式(4-1)表示的工作持续时间平均值,其方差为:
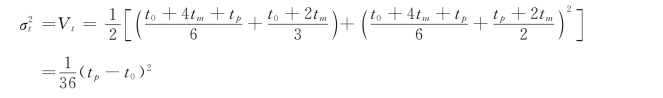
显然,当t0、tp越远离tm值,Vc越大,概率分布越离散,不确定性越大;当t0、tp越接近tm值,确定性越大。在极端情况下,当t0、tm、tp相同时,Vc为零,与关键线路法中相同,工作持续时间为一确定值。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




