下面通过算例说明工程总费用最小方案的确定。
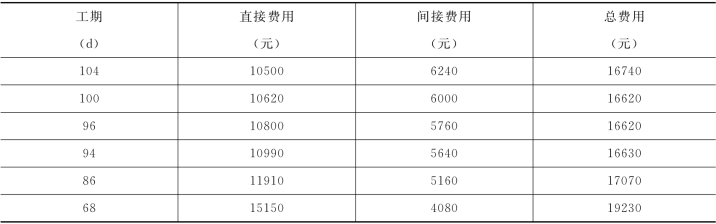
某工程项目计划的正常工期为104d,相应的最小直接费用为10500 元。在此基础上进行网络压缩(网络图及其压缩过程略),结果如表3-4 中的第一、第二列所示。由此可绘制出工程工期与工程直接费用的关系曲线,如图3-23 所示。
由于工程的间接费用可以近似等于间接费用变化率与工程工期的乘积,因此只要知道间接费用变化率i,即能方便地求出间接费用和间接费用曲线。若假设工程的间接费用变化率:
![]()
则不同工期下的总费用,绘成总费用曲线如图3-24 所示。总费用曲线上的最低点对应的工期为总费用最小的工程工期,对应的计划方案即为工程的总费用最小方案。

图3-23 工期与直接费用关系曲线
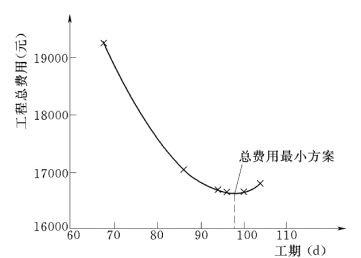
图3-24 总费用关系曲线
表3-4 计算数据
【例3-3】 已知某工程的初始网络计划如图3-25 所示。各工作的时间—费用关系如表3-5 所示。
(1)现要求工程10d完工,求工程量的最小直接费用方案。
(2)某施工单位承包了该工程。合同规定工期为12d,合同价为250 万元,若提前完工1d奖金9 万元,不计其他变更因素,求施工单位完成该工程的净效益最大方案。
表3-5 时间—费用关系表([例3-3]表)

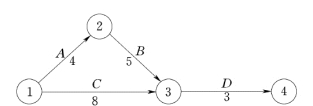
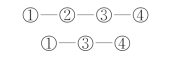
图3-25 网络图 ([例3-3]图)
解:根据表3-5 的资料,可计算出各工作的可压缩量tni-j-tci-j以及费用率。各工作的可压缩量分别为:
 (https://www.xing528.com)
(https://www.xing528.com)
各工作的费用率Si-j分别为:
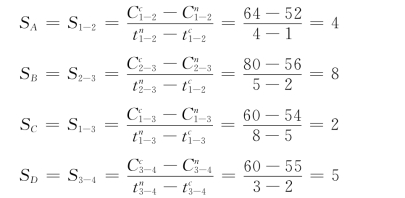
1.求10d工期要求下的最小直接费用方案
第一步:首先将各工作的正常持续时间、费用率、可压缩量分别标注在网络图上,如图3-26 (a)所示。这是工程的初始方案,工期为12d,直接费用为217 万元。关键线路为1-2-3-4,非关键工作C 的自由时差为FF1-3=1d。
第二步:在关键工作A、B、D 中选择费用率最小的工作A 进行压缩。
受最快持续时间限制,工作A 可以加快3d,但与其平行的非关键线路上的工作C 的自由时差只有1d,所以,只可以压缩工作A1d。压缩结果如图3-26 (b)所示,工期变为11d,不满足要求工期,直接费用增加到217 +1×4=221 万元。此时,关键线路有两条:
第三步:继续对图3-26 (b)所示方案压缩1d,有三个比较方案:
同时压缩工作A 及工作C 1d,费用率为2+4=6;
同时压缩工作B 及工作C 1d,费用率为2+8=10;
压缩工作D1d,费用率为5。
显然,第三方案最为合理,即压缩工作D1d,工期变为10d,费用增加到221+1×5=226 万元。压缩结果如图3-26 (c)所示。该方案为满足10d工期要求情况下的最小直接费用方案。
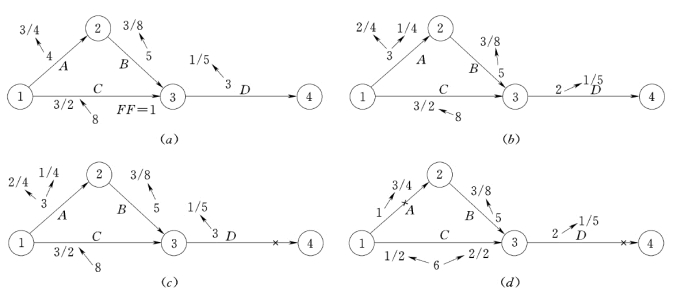
图3-26 网络计划图 ([例3-3]图)
2.求施工单位完成该工程的净效益最大方案
这一方案可以从初始网络计划开始,通过逐步压缩网络而得到。但本例中,问题 “1”的结果是可以利用的。在上述 “1”中的最后一步压缩中,费用率为5 万元/d,而本问题中提前完工1d奖金是9 万元,对施工单位来说是合算的。此时,施工单位的奖金净收益2×9- (1×4+1×5)=9 万元。所以,本例可以在图3-26 (c)的基础上进行继续压缩而求得最优方案。
继续压缩工作A、C 各2d,费用率为4+2=6 万元/元,而提前1d,得奖金9 万元,所以,是合算的。压缩结果如果3-26 (d)所示。
若考虑继续压缩网络计划如图3-26 (d),费用率最小的方案为同时压缩B、C 两工作,但费用率为10 万元/d,比能得到的奖金多,显然是不合适的。所以,图3-26 (d)所示的网络计划为施工单位完成该工程的净效益最大的方案,工期为8d。施工单位由于提前完工而所得净效益为
![]()
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




