水利工程建设直接费用优化方法

当所工序都采用最短时间时，我们可得到全部加快解，此时工期最短，但工程直接费用却是最高的。由于工程周期由关键工序决定，若非关键工序不采用最短时间，而采用大于最短时间的时间，甚至采用正常时间，这样既可以不影响工程周期，又能降低工程的直接费用。如图3-19 中，最短时间最小费用解B 点与全部加快解C 点工期相等，但费用少很多。下面介绍的费用优化方法，就是以正常费用解为初始方案，通过逐步压缩，找出不同工期下的最低直接费用方案。

1.网络的压缩

在一项工程计划中，当每项工作均以最少的费用和正常的持续时间来完成时，即得到正常的工期及相应的工程直接费用。如果希望缩短工期，就需要加快某些工作的完成时间或者压缩工作的持续时间，费用也会相应增加。这种缩短工作持续时间的做法称为工作的压缩。要求得到最优解，就需要对各项工作的压缩进行比较。现以图3-20 的简单网络图说明如下：

希望缩短工期，但最多允许增加费用100 元，问如何安排可使工期缩短最多？

显然，工作A 的非关键工作，可不考虑对其压缩。只有压缩关键路线上的工作B、C才是有效的。100 元钱全部用于压缩工作B，可缩短工期1d；全部用于压缩工作C，可缩短工期2d。所以，最好的方案是将100 元钱全部用于工作C，使其持续时间加快到2d，从而工期缩短到18d。

综上所述，可以按下述规则来选择压缩工作对象，即：在进行网络压缩时，优先压缩费用率最低的关键工作。

2.网络压缩的约束限制

通过上述分析，可得到一条选择压缩工作对象的规则，但该工作究竟可以压缩多长时间，可能受到以下的约束限制：

（1）工作本身的最快持续时间的限制。每个工作只能加快到它的最快持续时间，这是工作压缩的极限。设i－j 工作的现在持续时间为ti－j，那么该工作最多可以压缩的时间为。

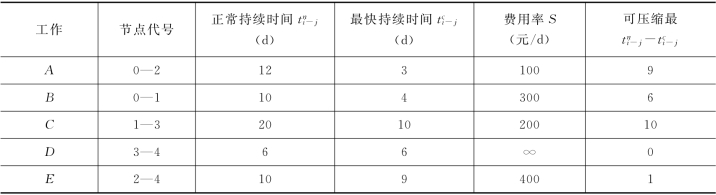
图3-22 （a）为一个初始网络计划。计划中各工作都采用正常持续时间，分别标在相应工作箭线旁。各工作的持续时间—费用关系，如表3-3 所示。为便于图上计算，在各项工作旁还标出该工作最多可压缩的时间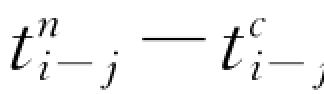及费用率S。例如工作B 旁标有：

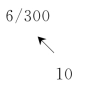
表示该工作现在的工作持续时间为10d，还可以加快6d，其费用率为300 元／d。箭头“↖”应指向左上方。对于某些由于某种原因不能加快的工作或者某些已经加快到极限的工作，在其箭上标“×”号。

表3-3　工作持续时间—费用关系表

在图3-22 （a）中，关键路线为：

在关键工作中，工作C 的费用率为200 元／d 最小，可以压缩10d，与该关键线路平行的非关键线路上的工作E 有14d自由时差，所以可以将工作C 压缩10d。此时工作C 已不能再压缩，故在其箭线上标以“×”号，并将标注改为：

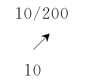
表示工作C 已加快了10d，费用率200 元／d，现在持续时间为10d。标注箭头应指向右上方。此时，工程工期变成了26d，费用增加了10×200＝2000 元。

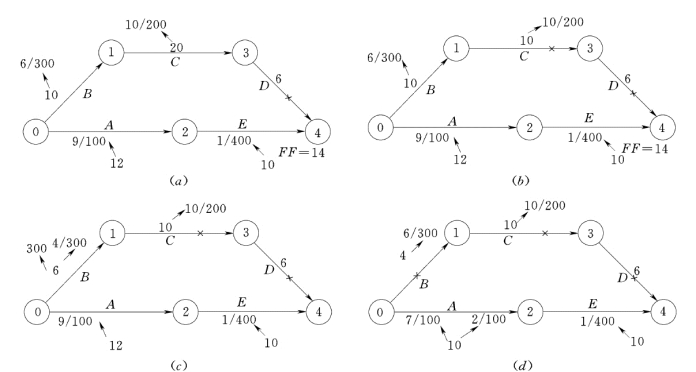
图3-22　纯压缩法步骤图

（2）非关键工作时差的限制。在关键线路上可以压缩的数值超过平行非关键线路上最后一项工作的时差值的情况下，它的压缩值就受到时差的限制。如图3-22 （b）所示情况下，如果要继续压缩关键工作B，它本身可能压缩的天数为6d，费用率为300 元／d。但在非关键线路上的工作E，局部时差只有4d，所以工作B 受到这一限制只能压缩4d，使总工期缩短到22d，费用再增加4×300＝1200 元。此时两条线路的线路总时间相等，均成为关键线路。工作B 旁的标记改为：

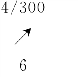(www.xing528.com)

表示工作B 现在持续时间为6d，已加快了4d，还可以加快2d，费用率为300 元／d，如图3-22 （c）所示。

（3）平行关键线路的约束限制。当一个网络图中存在两条（或数条）关键线路时，如果需要缩短整个工程的工期，必须同时在两条 （或数条）。例如图3-22 （c）的网络中两条线路上压缩相同的天数。例如图3-22 （c）的网络中两条线路均为关键线路，如需再缩短工期，就必须同时压缩工作B 及另一条关键线路上费用率最低的工作A。工作A 可能压缩值为9d，但工作B 只能压缩2d就达到最快持续时间的极限，所以工作A 只能与工作B 同时压缩2d，使工期缩短到20d [图3-22 （d）]，相应再增加费用2× （300＋100）＝800 元。

（4）紧缩的关键线路的结束限制。当关键线路的各项工作的持续时间都已达到最快持续时间，这条线路就称为“紧缩的”关键线路（Grashed Critical Path）。在网络中存在这种紧缩的关键线路时[如图3-22 （d）中的B—C—D]，整个网络就不宜再进行压缩了。因为在这种情况下，再压缩任何工作都不能有效地达到缩短工期的目的，反而会无益地增加费用，如图3-20 中B—C 段。

3.网络计划的简化

从前面的分析可知，网络计划的费用优化过程非常复杂，而优化计算之前，得到每项工作缩短持续时间的各种方案的工作量则更大。因此，在网络计划优化之前，从计划中暂时删去那些满足规定工期条件下始终不能转变为关键工作的非关键工作，可大大减少网络计划优化的工作量。本章第一节中介绍的选择压缩工作对象的原则，可用来简化网络图。以下介绍的通过网络计划时间参数计算简化网络图的效果则更好，主要有两种方法。

方法一：

（1）先计算各项工作的最早开始时间和最早完成时间，计算出网络计划的计算工期Tc。

（2）将计划工期Tp规定为项目的要求工期，计算各项工作的最迟开始时间和最迟完成时间。

（3）计算各项工作的总时差。

（4）总时差大于等于零的工作是在满足规定工期情况下，不需要缩短持续时间的工作，可以从计划中简化去。

方法二：

（1）按工作正常持续时间找出关键工作及关键线路。

（2）令各关键工作都采用其最短持续时间，并进行时间参数计算，找出新的关键工作及关键线路。

重复此步骤直到不能增加新的关键线路为止。

（3）删去不能成为关键工作的那些工作，将余下工作的持续时间恢复为正常持续时间，组成新的简化网络计划。

4.网络压缩的步骤

（1）简化网络计划。

（2）计算网络计划中各工作的费用率Si－j。

（3）在简化了的网络计划中找出费用率 （或组合平行压缩不同线路上工作的费用率）最低的一项或一组关键工作，作为缩短持续时间的对象。

（4）考虑网络压缩的限制，确定可压缩量。

（5）计算整个网络的压缩后的新工期及不能再压缩或者满足要求工期为止。

应当指出的是：在 （1）中简化去的工作，在最后确定优化方案后应添补出来。