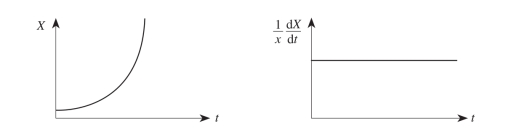
图2.18 生态系统指数增长模式
来源:王飞儿《生态城市理论及其可持续发展研究》
王飞儿分析了城市生态系统的发展速度和发展过程(图2.18、图2.19)。在Logistic方程基础上,城市生态系统的发展轨迹划分为起步期、发展期、成熟期和顶峰期(表2.3),指出发展期和成熟期系统是可持续的。并进一步指出城市生态系统的可持续性通过对系统的协调和控制,可以使系统发展步入良性的循环轨道,但如果协调和控制不成功,系统发展将会走向衰退。可以通过延长发展期和成熟期、增大系统的阈值(生态承载力)等来实现城市生态系统的可持续发展[5]。
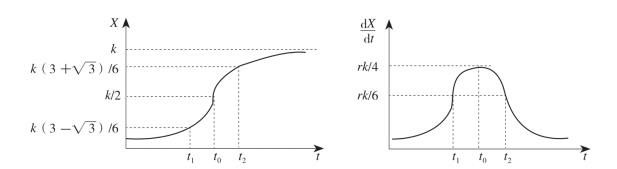
图2.19 城市发展过程和发展速度曲线图
来源:王飞儿《生态城市理论及其可持续发展研究》
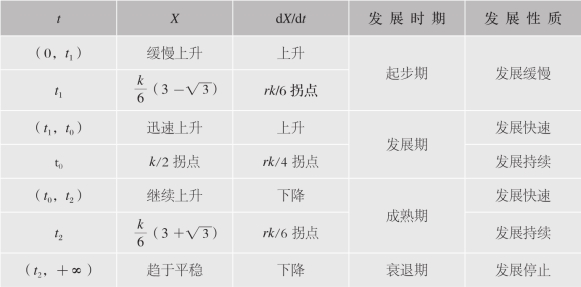
来源:王飞儿《生态城市理论及其可持续发展研究》
表2.3 基于Logistic曲线的城市生态系统发展轨迹
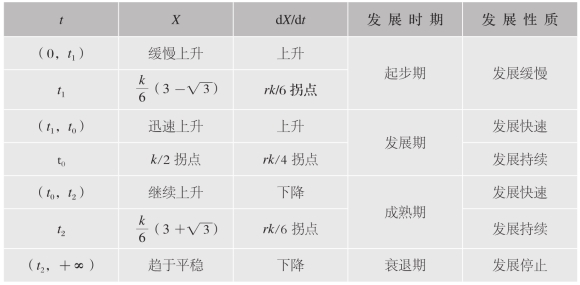
生态城市是高效、和谐、健康、可持续发展的人类聚居环境,也是城市生态系统进化的方向。运用Logistic方程可以计算出城市生态系统的发展轨迹:将Logistic曲线划分为4个阶段,即起步期、发展期、成熟期和顶峰期,通过分析可以得出在发展期和成熟期的系统是可持续的,在实施可持续发展战略时,尽可能延长这一时期。
城市生态系统的可持续性发展调控可以通过延长发展期和成熟期、增大系统的阈值(生态承载力)、内在强机制适当“弱”化与内在弱机制适当“强”化等,最终达到整个系统的可持续发展。
通过对环境生态学、传统聚落空间形态、分形理论、人居环境科学理论、生态可持续发展理论的相关研究理论进行解析,针对它们在传统聚落空间形态的研究现状,对当前的一些技术策略与研究方法进行总结,主要归纳为以下几个方面的特点:
(1)环境生态学作为环境科学与生态学的交叉学科,从生态学的角度构建传统聚落的生态系统,从环境科学的角度提供改善环境的技术策略,为本研究传统聚落生态系统可持续发展提供了重要的基础理论。
以城市生态系统的可持续发展模型为依据,构建传统聚落生态系统的可持续发展。将传统聚落生态系统的发展保持在发展期和成熟期区域,通过调控等策略形成生态可持续发展。并以此为基础,对传统聚落空间形态进行分析和优化设计,以形成传统聚落空间形态的生态可持续发展。生态修复手段对当前环洱海区域传统聚落空间形态的演变产生了重要影响。生态修复是环境生态学中改善环境的一种重要技术手段。生态修复技术与策略对环洱海区域传统聚落空间形态的生态可持续发展具有重要的推动作用,将传统聚落的空间形态要素与生态修复相结合进行规划设计具有积极的意义。
(2)分形理论已被广泛运用于不同的研究领域。传统聚落因其所处的地理位置与形成背景不同,具有灵活的空间形态。作为空间形态分析可量化的研究方法之一,将分形理论运用于传统聚落空间的平面形态、街巷空间、公共建筑、民居空间等的研究。通过分析比较不同历史时期传统聚落空间形态的特征,可以得出环洱海区域传统聚落的环境生态观,分析当代传统聚落空间形态的演变特征,以及探讨传统聚落空间形态可持续发展的策略与设计方法。
(3)将人居环境科学理论与环洱海区域传统聚落的环境生态观相结合,共同探讨环洱海区域传统聚落的人居环境科学思想。深入分析人居环境科学的自然系统、人类系统、社会系统、居住系统和支撑系统,以此为基础,归纳、总结环洱海区域传统聚落环境生态观。
(4)以生态可持续发展理论为基础,结合环洱海区域传统聚落的环境生态观、当代传统聚落空间形态演变特征,运用环境生态学的生态系统理论与环境技术策略,科学地构建环洱海区域传统聚落生态模型,探讨环洱海区域传统聚落空间形态的生态可持续发展。
综上所述,构建本书的研究体系解析模型(图2.20):以环境生态理论中的生态系统与生态修复为研究视角,以传统聚落不同时期、不同类型与不同层级的空间形态为研究对象,并将分形理论中的分形维数作为研究方法,将人居环境科学理论与生态可持续发展理论相结合,尝试构建传统聚落的生态可持续模型。(https://www.xing528.com)
以此研究体系作为研究理论基础,对环洱海区域传统聚落的空间形态演变展开研究。
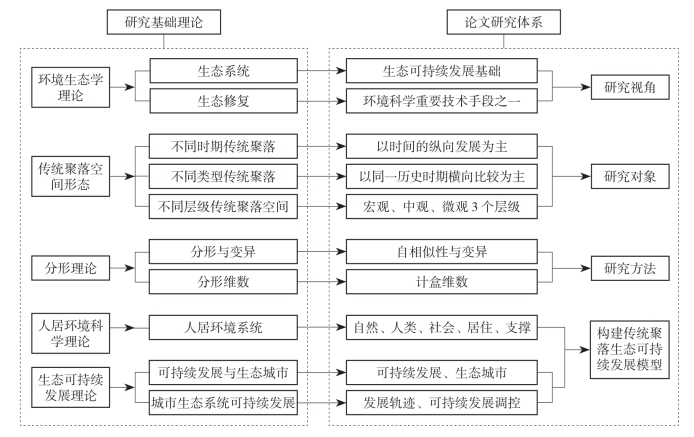
图2.20 本书的研究体系解析模型
【注释】
[1]北京大学社会科学与社会研究中心.马克思主义与自然科学[M].北京:北京大学出版社,1988:244.
[2]此部分内容为笔者主要根据中国知网整理,由于数据更新较快,本研究数据截至2020年3月9日,图表内容仅供参考。
[3]人们习惯将点定义为0维,将直线定义为一维,将平面定义为二维,将空间定义为三维,爱因斯坦在相对论中引入时间维,形成四维时空。数学上,把欧氏空间的几何对象连续地拉伸、压缩、扭曲,维数也不变,这就是拓扑维数。分形体不同于一般的欧氏几何体,其维数介于点、线、面之间,往往是分数。为了定量地描述客观事物的“非规则”程度,数学家豪斯多夫(Hausdorff)于1919年提出了连续空间的概念,即空间维数不是跃变的,而是可以连续变化的,既可以是整数,也可以是分数,称为豪斯多夫维数,记为Df。为了表达分形的分数性质,Benoit B.Mandelbrot把豪斯多夫维数称为分形维数。分形维数推广了传统的几何维数概念,突破了维数必须是整数这一局限,使得分形几何不仅能够描述有特征大小或尺度的人造对象,而且能够描述雪花、云彩、树枝、烟雾、火光等没有特定大小或比例的自然形状。
[4]联合国正式文件.第四十七届会议通过的决议和决定[EB/OL].https://www.un.org.
[5]王飞儿将城市生态系统的发展轨迹表示为以下几个公式:
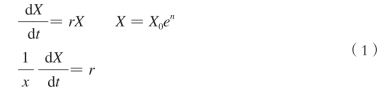

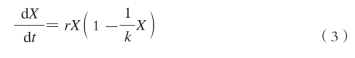
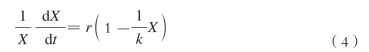
![]()
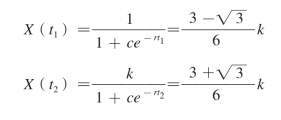

![]()
![]()
![]()
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




