2.3.2.1 分形的性质
英国数学家肯尼思·法尔科内(Kenneth Falconer)提出分形集的基本性质,如果集合F具有以下所有或大部分的性质,则它就是分形:具有精细的结构;具有不规则性;具有自相似性;分维值大于它的拓扑维数;多以简单方法定义,可由迭代生成。
2.3.2.2 自相似性
分形理论的重要原则是自相似和迭代生成。自相似性(self-similarity)指某一结构或过程的特征从不同的空间尺度或时间尺度来看都是相似的,或者某系统或结构的局部性或局部结构与整体类似,体现了分形具有跨越不同尺度的对称性。自然界的分形包括规则分形和随机分形。规则分形是按一定规则精心构造出来,可以不断递推下去以至无穷,它们严格满足自相似性,是自相似分形集,如科契(Koch)雪花曲线(图2.8)、谢尔宾斯基(Sierpinski)地毯曲线(图2.9)等,规则分形是少数。无规则分形(随机分形)在大自然中大量存在,如蜿蜒曲折的海岸线(图2.10)。无规则分形反映自然现象所具有的随机的不光滑性和不规则性,它们仅具有近似的或统计意义下的自相似性。
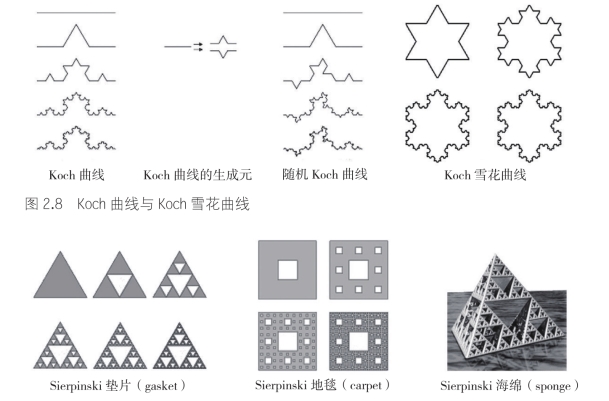
图2.9 Sierpinski垫片、Sierpinski地毯和Sierpinski海绵
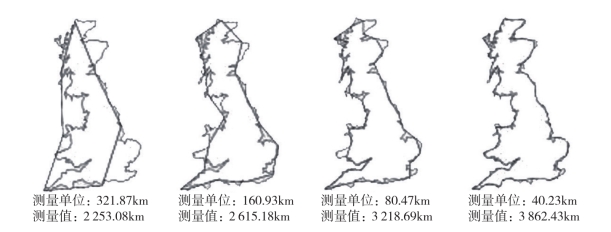
图2.10 Benoit B.Mandelbrot测量“英国海岸线有多长”图示
图2.8、图2.9、图2.10来源:赵远鹏《分形几何在建筑中的应用》
2.3.2.3 分形的生成
分形的构成方法有:基于L系统的分形模型、迭代函数系统模型、粒子系统模型和随机插值模型。分形几何具有无限和统计自相似性规律,它用递归算法将复杂景物简化生成,可产生任意水平的细节,提供描述一般形状的数学模型。分形在计算机图形学中的应用,是借助分形模型精细刻画传统几何学难以描述的景物。目前最常用的随机过程是分数布朗运动,它具有统计自相似性,构造过程简单,便于计算机快速迭代。
分形图案的复杂性来自简单数学关系的反复迭代。分形理论认为复杂的对象可能只遵从简单的规则,一旦知道这些简单的规则就可以直接生成整体结构。整个结构中可以发现各种各样的自相似结构,某个部分重复了另一个部分的式样或者整体与部分有嵌套关系。分形迭代是将待生成的图像看成是由许多与整体相似的或经过一定变换与整体相似的小块拼贴而成。
2.3.2.4 分形维数
1)分形维数的含义(https://www.xing528.com)
分形维数(fractal dimension)指分形结构的自相似程度、不规则程度或破碎程度的定量参数。它又称分维或分维数,通常用分数或带小数点的数表示。它是分形几何理论中最重要和最核心的内容[3]。通常,二维空间中的一个分维数曲线介于1和2之间,三维空间中的一个分维数曲线介于1和3之间。分维数的引入为研究复杂形体提供了全新的角度,使人们从无序中发现了有序,许多学科将分维数作为解决难题的新工具。
2)分形维数的计算和测定
分形维数是分形几何理论的核心之一,是描述分形体复杂结构的主要工具。其变化是连续的,它定量描述分形结构自相似度、不规则程度或破碎程度。目前有许多分形维数的定义和计算方法,主要包括豪斯多夫维数(Hausdorff dimension)、盒维数(box counting dimension)、容量维数、信息维数等。而盒维数及其变形则由于易于进行程序化计算,在分形理论应用研究中得到广泛应用。计盒维数是用一个个的小分格来划分分形体,从相交的盒子数及划分单位的关系来计算分维(图2.11),分段N就可以看成是曲线与盒子相交的格子总数,N和r满足式(2-1):
![]()
式中,ε——线尺度缩小的倍数;
N(ε)——曲线和盒子的相交总数;
D——分形维数;
A——表示常数项。
可见,lnN(ε)和ln(ε)呈线性关系。分形维数的测试方法有多种,如计盒数法、小岛法(Slit island method)、垂直截面法(或步长法,vertical section method)、扫描二次电子法等。
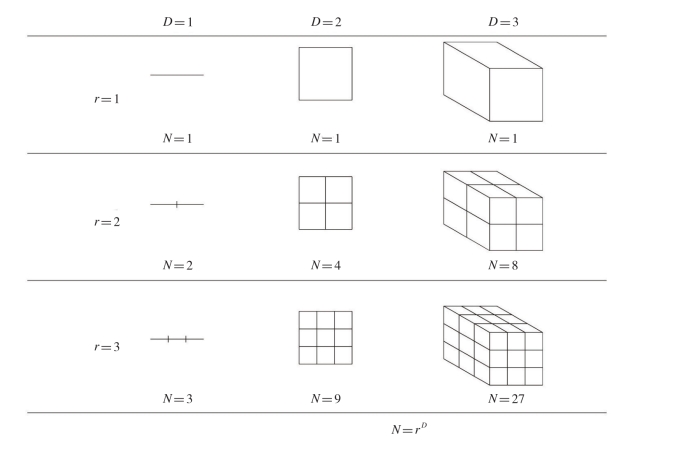
图2.11 分形维数的计算
来源:邹明清《分形理论的若干应用》
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




