大学物理学：长度收缩成果

在伽利略变换中，物体的长度不随惯性系的改变而改变.在洛伦兹变换中，情况又如何呢？

设有两个观察者分别静止于惯性参考系S 和S′中，惯性参考系S′以相对S 系速度v 沿Ox 轴正方向匀速运动.一细杆静止于S′参考系中并沿Ox′轴放置，如图13.6 所示.

将观察者相对于杆静止时测得的长度l0 称为杆的固有长度.考虑到杆的长度应是在同一时刻测得的杆两端点的距离，因此，S′参考系中观察者若同时测得杆两端点的坐标分别为x′1和x′2，则杆的长度为l′＝x′2－x′1，此时有l′＝l0.而S 参考系中的观察者则认为杆相对于S 参考系以速度v 运动，并同时测得其两端点的坐标分别为x1 和x2，即S 参考系中的观察者测得杆的长度为l＝x2－x1.利用洛伦兹变坐标换式（13.11），有

图13.6　长度收缩

式中t1 ＝t2，将上两式相减，得

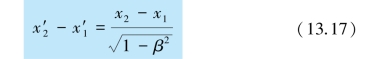
即

这就是说，对于相对运动速度较小的惯性参考系来说，长度可以近似看作一绝对量.在地球上，宏观物体运动所达到的最大速度与光速之比约为10－5.在这样的速度下，长度的相对收缩，其数量级约为10－10，可以忽略不计.

例13.1　设想有一光子火箭，相对地球以速率v ＝0.95c 做直线运动.若以火箭为参考系测得火箭长为15 m.问以地球为参考系，此火箭的长度.

解　根据式（13.18）有

即从地球测得光子火箭的长度仅为4.68 m.(www.xing528.com)

解　设一杆静止于S′系，长度为l′，它与O′x′轴得夹角为θ′.此杆长在O′x′和O′y′轴上的分量分别为

由于S′系沿Oy 轴相对S 系的速度为零，故从S 系的观察者来看，此杆在Oy 轴上的分量ly 与l′y相等，保持不变，即

图13.7

而杆在Ox 轴上的分量，由式（13.18），有

因此，从S 系中的观察者来看，杆的长度为

而杆与Ox 轴的夹角θ 由下式确定：

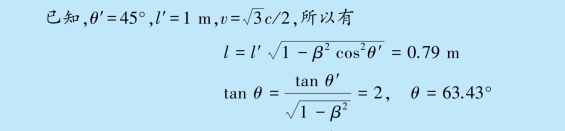
可见，从S 系中的观察者来看，运动着的杆不仅长度要收缩，而且还要转向.