大学物理学迈克耳孙-莫雷实验

伽利略变换和牛顿力学相对性原理在物体低速运动范围内与实际情况高度相符.然而，19 世纪末，作为电磁学基本规律的麦克斯韦方程组得到确立，它的一个重要成果就是预言了电磁波的存在，并证明了电磁波在真空中的传播速度等于真空中的光速c，从而揭示了光的电磁本性.根据麦克斯韦方程组可知，光在真空中的传播速度在所有的惯性参考系中都是相同的，这显然与伽利略速度变换相矛盾.适用于所有力学规律的力学相对性原理，在研究光的传播时遇到了困难.因此，力学相对性原理和麦克斯韦电磁场理论中，至少有一个是不正确的.由于牛顿在物理学界的影响，很多人相信力学相对性原理是正确的，而麦克斯韦电磁理论只能在一个特殊的惯性参考系中成立，这个惯性参考系称为以太参考系.那时认为以太充满整个空间，即使真空也不例外.在相对以太静止的参考系中，光沿各个方向的传播速度都是c，于是，以太参考系就可以作为绝对参考系.若有一运动参考系，它相对于绝对参考系以速度v 运动，那么，由牛顿力学的相对性原理，光在运动参考系中的速度应为

其中c 是光在以太这一绝对参考系中的速度，c′为光在运动参考系中的速度.从上式可以看出，在运动参考系中，光的速度在各个方向是不同的.

如果能借助某种方法测出运动参考系相对于以太的速度，那么，作为绝对参考系的以太也就被确定了.为此，历史上曾有许多物理学家做过很多实验来寻找绝对参考系，但都得出了否定的结果.其中最著名的是1887 年迈克耳孙和莫雷所设计的实验.实验的基本思路是：假如以太参考系真实存在，地球应该在以太中运动，那么这种运动应该影响光相对于地球的速度，并且产生一些可观察的光学效应，使我们能够确定地球相对于以太的运动.

迈克耳孙—莫雷实验装置如图13.3（a）所示.由光源S 发出波长为λ 的光，入射到半反半透镜G 后，一部分光反射到平面镜M2 上，再由M2 反射回来透过半反半透镜G 到达望远镜T；另一部分光则透过半反半透G 到达M1，再由M1 和G 反射也到达望远镜T.假定G 到平面镜M1 和M2 的距离均为l（l 称为有效臂长），且M1 和M2 不严格垂直，那么，在望远镜的目镜中将看到干涉条纹.

把固定在地球上的整个实验装置作为运动参考系，假设它相对于绝对参考系（以太参考系）以速度v 运动.而从运动参考系来看，以太则以－v 的速度相对运动参考系运动，光在以太中不论沿哪个方向的速度均为c.若取以太参考系为S 系，运动参考系为S′系，那么根据式（13.4），从S′系来看，光自G 到M1 速度为c－v，而光自M1 到G 速度为c＋v，于是，从S′系来看，光自G 到M1，然后再由M1 回到G 所需时间为

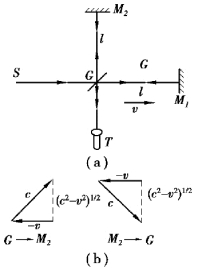
图13.3　迈克耳孙—莫雷实验

由式（13.5）和式（13.6）可以看出从S′系来看，G 点发出的两束光到达望远镜的时间差为

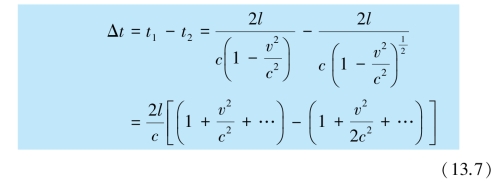(www.xing528.com)

由于v≪c，上式可写成

于是，两光束汇合时的光程差为

若把整个仪器旋转90°，那么两束光汇合时的光程差将变为－δ，即前后两次测量中光程差的该变量为2δ.因此，在转动过程中，望远镜内看到的干涉条纹将会移动，移动条数为

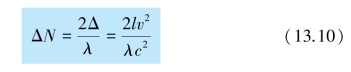
式中λ、c 和l 均为已知，如能测出条纹移动的条数ΔN，即可由式（13.10）算出地球相对于以太的绝对速度v，从而就可以把以太作为绝对参考系了.

在迈克耳孙—莫雷实验中，若取干涉仪有效臂长l 约为10 m，钠光波长λ ＝500 nm，v 取地球公转的速度（3×104 m／s），那么可由式（13.10）估算出干涉条纹移动的条数约为0.4.但是，在实验中没有观察到这个预期的条纹移动.改变实验环境，进行了多次实验，始终没有得到预期的结果.

当时，许多科学家在不同的季节、不同的条件下重复迈克耳孙—莫雷实验，其结论是：无法测出地球相对于以太参考系的绝对速度.但是很少有人怀疑伽利略变换的正确性，因此他们都失败了.英国物理学家开尔文（L. Kelvin， 1824—1907）把这一疑惑说成是在物理学晴朗的天空中的“一朵乌云”.迈克耳孙—莫雷实验的结果使我们看到，要解决力学相对性原理和电磁理论的矛盾，出路只有一条：必须放弃经典时空观，建立新的时空观.1905 年，爱因斯坦另辟蹊径，通过对时空本性以及电磁理论的深刻考察，提出狭义相对论.根据爱因斯坦狭义相对论的基本假设，尤其是光速不变原理，很容易解释迈克耳孙—莫雷实验的结果.