大学物理学杨氏干涉实验结果

1801 年，托马斯·杨巧妙地设计了一种把单个波阵面分解为两个波阵面以锁定两个光源之间相位差的方法来研究光的干涉现象.杨氏用光的叠加原理解释了干涉现象，在历史上第一次测定了光的波长，为光的波动学说的确立奠定了基础.

1）杨氏双缝干涉的实验装置

杨氏双缝干涉的实验装置如图12.28（a）所示.将一束平行单色光照射到狭缝S 上，S 相当于一个线光源，狭缝S 后又放有与S平行且等距离的两个平行狭缝S1 和S2.两狭缝的距离很小，可以构成一对相干光源，S1、S2 发出的光波在空间叠加，产生干涉现象.如果在双缝后放置一白屏，白屏上有等距离的明暗相间条纹出现.当然，用小孔代替狭缝，同样可以得到明暗相间的干涉条纹.这些干涉实验统称为杨氏实验.杨氏干涉实验的成功，为光的波动理论确定了实验基础.由于S1 和S2 是从S 发出的波阵面上取出的两部分，所以把这种获得相干光的方法称为分波阵面法.

2）明暗条纹的位置和条纹间距

现在对屏幕上干涉条纹的位置作定量的分析.如图12.28（b）所示，设双缝间的距离为d，双缝至屏的距离为D（D≫d）.考察光屏上的某一点P，从S1 和S2 到P 点的距离分别为r1 和r2.若双缝的中垂线与屏交于O 点，以O 为原点，取坐标轴OX，P 点的坐标为x.由于从S 到S1 和S2 的距离相同，所以S1 和S2 是两个同相光源.因此P 点处两光波的光程差仅由从S1 和S2 到P 点的波程差决定.由几何关系可知，在近轴和远场近似条件下，即r ≫d 和r ≫λ的情况下，有

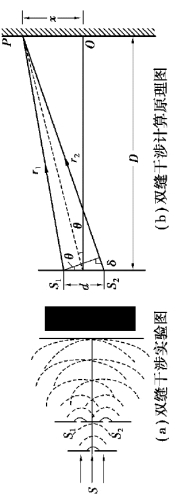
图12.28　杨氏双缝干涉

式中，θ 是P 点的方位角，即S1S2 的中垂线MO 与MP 之间的夹角.通常情况下，这一夹角很小，故有sin θ≈tan θ.此时，波程差∆r可以写作

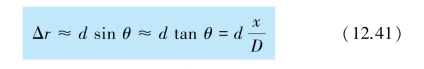
当实验装置处在空气中时，折射率n ＝1.此时，光程差δ 和波程差∆r 相等，即

由于从S1 和S2 发出的光传向P 的方向几乎相同，它们在P点引起的振动的方向近似相同.根据同方向振动的叠加规律，当从S1 和S2 发出的光到达P 点的光程差为波长λ 的整数倍，即

亦即从S1 和S2 发出的光到达P 点的相位差为

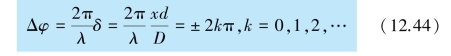
时，两束光在P 点叠加的合振幅最大，亦即呈现干涉相长，P 点出现明条纹.由式（12.43）、式（12.44）可以得到k 级明条纹中心在X轴上的位置，即

其中k 称为明条纹的级次.k ＝0 的明条纹称为零级明条纹或中央明纹，k ＝1，2，…分别称为1 级明条纹、2 级明条纹、……式中正负号表示各级干涉条纹对称分布在中央明纹的两侧.

亦即从S1 和S2 发出的光到达P 点的相位差为

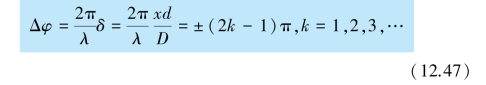
时，两束光在P 点叠加的合振幅最小，亦即呈现干涉相消，P 点形成暗条纹.同样，可以得到暗条纹中心在X 轴上的坐标位置为

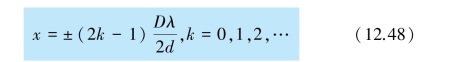
式中，k ＝1，2，…分别对应第1 级暗条纹、第2 级暗条纹、……光程差为其他值时，干涉条纹的亮度介于明条纹和暗条纹之间.

规定：两相邻明条纹中心或两相邻暗条纹中心之间的距离为条纹间距.由式（12.46）或式（12.49）可以求出两相邻明条纹或两相邻暗条纹的间距为

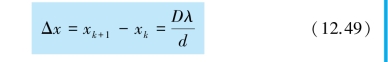
由式（12.50）可知，Δx 与k 无关，因此干涉条纹是等间距地分布于中央明纹的两侧.实验中必须使D 足够大，d 足够小，否则干涉条纹过密，以致无法分辨.

在实际工程技术中，杨氏双缝干涉实验装置采用单色波入射，若能测出双缝间隔d，双缝与屏幕间距D 以及条纹在光屏上的位置x 或条纹间距Δx，就可以计算出单色波长λ.历史上，托马斯·杨正是通过双缝干涉实验第一次测定了可见光的波长.若在实验中，用一透明薄片覆盖其中一缝，干涉条纹会发生移动，根据移动的条纹数目或移动的距离，薄片折射率，以及实验装置参数，可求得薄片的厚度，或根据薄片的厚度求得薄片折射率.

例12.4　在杨氏双缝干涉实验中，屏与双缝间的距离D＝0.7 m，用He⁃Ne 激光器作为单色光源（λ ＝632.8 nm），问：

（1）d ＝2 mm 和d ＝5 mm 两种情况下，相邻明纹间距各为多少？(www.xing528.com)

（2）如肉眼仅能分辨两条纹的间距为0.15 mm，现用肉眼观察干涉条纹，问双缝的最大间距是多少？

解　（1）由式（12.50）知，相邻两明纹间的距离为

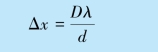
当d ＝2 mm 时

当d ＝5 mm 时

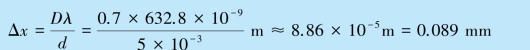
（2）当Δx ＝0.15 mm 时，双缝间距为

可以看出，在这样的条件下，双缝间距必须小于3 mm，肉眼才能看到干涉条纹.

例12.5　在杨氏双缝实验中，双缝间距为1.5 mm，光屏离双缝的距离为1 000 mm，当用一片折射率为1.5 的透明薄片遮挡住其中一条缝，如图12.29 所示，发现光屏上的条纹系统移动了5 mm.试求薄片的厚度.

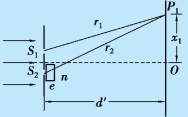
图12.29　例12.5 用图

解　没放薄片时，条纹位置

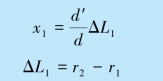
放薄片后，条纹位置

覆盖一条缝后，条纹移动距离

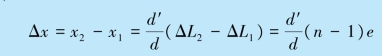
可得薄膜厚度

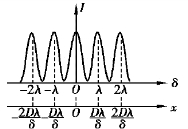
图12.30　双缝干涉的光强分布

3）杨氏双缝干涉图样的特点

由式（12.46）和式（12.49）可知，双缝干涉条纹等间距地分布于中央明条纹的两侧.根据式（12.37）及双缝干涉公式可以得到白屏上干涉条纹的光强分布曲线，如图12.30 所示.

在狭缝间距和狭缝到屏的距离确定的情况下，条纹在屏幕上的位置和间距取决于入射光的波长.因此，当采用平行的白光入射，干涉条纹的中央明纹仍为白色，其两侧各种波长的同一级明纹彼此错开而呈现由紫到红的彩色条纹.

对于两种不同的光波，若其波长满足k1λ1 ＝k2λ2，则λ1 的第k1 级明条纹与λ2 的第k2 级明条纹在同一位置上，这种现象称为干涉条纹的重叠.

级次增加时，不同级的条纹发生重叠，看到的是由混合色光形成的彩色条纹.