平面上光的折射成像-大学物理学

与平面反射成像不同，折射光的折射角与入射角为非线性变化，折射光线的反向延长线一般不会相交于一点，如图12.4 所示。

光束的同心性被破坏了，因此不能形成清晰的像，这种现象称为像散.然而，生活经验告诉我们，如果水中有一发光点，在水面上可以看到比较清晰的像，这是因为人眼的瞳孔只让折射光中极细的一束进入人们的眼内，此时相应的i 和r 必然很小，因此有

把它们代入式（12.5）可得

式（12.7）表明，在小光束范围内所有折射光线的反向延长线近似交于同一点S′，S′与入射角无关，S′是一个像点.因为S′是发散光线反向延长线的交点，所以S′为虚像.由于n1 ＞n2，故像距p′小于物距p.p′称为视深度.用于矫正视力的近视镜与远视镜也是依据此原理。

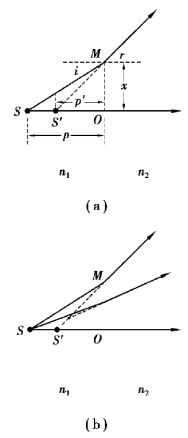
图12.4　平面折射成像重新插入图片

例12.1　如图12.5 所示，单色光入射一折射棱角A 为60°的玻璃三棱镜，玻璃的折射率为1.6.若入射角为i1，求出射光线和入射光线之间的夹角（偏向角）.

解　从图12.5 中可以看出：

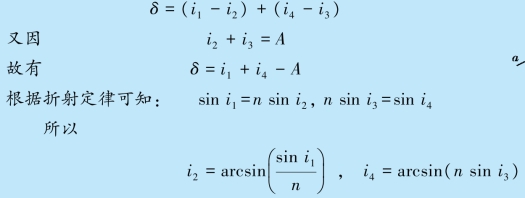
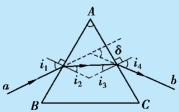
图12.5　例12.1 用图

把i3 ＝A－i2 代入上式，可得(www.xing528.com)

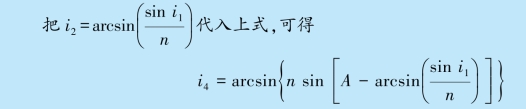
把i4 代入δ＝i1＋i4－A，可得

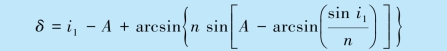
可以证明，当i1 ＝i4 时，偏向角达到最小值，因此将i1 ＝i4 代入上式，即得最小偏向角为

最小偏向角对应的入射角为

又因i1 ＝i4 时，折射角为

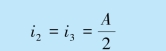
所以，利用特殊的入射角和最小偏向角可以计算棱镜的折射率，即

因此，只要测出最小偏向角就可以确定棱柱形透明介质的折射率.这里之所以用最小偏向角而不用任意偏向角，是因为它在实验中最容易精确测量.