大学物理学（下册）：位移电流

在恒定电路中传导电流是处处连续的，在这种电流产生的恒定磁场中，安培环路定理可以写成

图11.19　位移电流

而对于仍然以L 为周界的曲面S2，它延展到了电容器两极板之间，又不与导线相交，由于不论是充电还是放电，穿过该曲面的传导电流都为零，所以有

显然，这两个结论是相互矛盾的.在电容器充放电的过程中，对整个电路来说，传导电流是不连续的.安培环路定理在非恒定磁场中出现了矛盾的情况，必须加以修正.可以选择的修正方案有两种：①放弃传导电流连续性；②放弃电荷守恒定律.电荷守恒定律是普适规律，而传导电流的连续性是在恒定条件下实验总结出来的特殊规律.因此，麦克斯韦选择放弃传导电流的连续性，而提出位移电流假设来解决这一矛盾.

通过对电容器充放电过程的分析可以发现，虽然传导电流在电容器两个极板之间中断了，但与此同时，两个极板之间却出现了变化的电场.电容器极板上自由电荷q 随时间变化形成传导电流的同时，极板间的电场E、电位移矢量D 也在随时间变化着.由于

将上式对时间求导

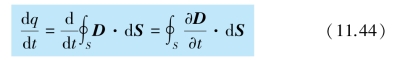
于是得

为位移电流密度，即电场中某点的位移电流密度等于该点电位移矢量随时间的变化率，而

为位移电流，即通过电场中某截面的位移电流等于位移电流密度在该截面上的通量，或者说，位移电流在数值上等于穿过任一曲面的电位移通量的时间变化率.

按照麦克斯韦的假设，在含有电容器的电路中，电容器极板表面中断的传导电流I，可以由位移电流Id 替代，二者合在一起维持了电路中电流的连续性.麦克斯韦认为，传导电流I 和位移电流Id 可以共存，两者之和称为全电流，即

(www.xing528.com)

引入了位移电流后，麦克斯韦把从恒定电流的磁场中总结出来的安培环路定理推广到非恒定电流情况下更一般的形式，即

式（11.50）表明，磁场强度H 沿任意闭合回路的线积分等于穿过此闭合回路所包围曲面的全电流，这就是全电流的安培环路定理.

虽然位移电流和传导电流在激发磁场方面是等效的，但它们却是两个不同的概念.传导电流是大量自由电荷的宏观定向运动，而位移电流的实质却是关于电场的变化率.传导电流通过电阻时会产生焦耳热，而位移电流没有热效应.

位移电流的引入深刻揭露了电场和磁场的内在联系和依存关系，反映了自然现象的对称性.法拉第电磁感应定律说明变化的磁场能激发涡旋电场，位移电流的论点说明变化的电场能激发涡旋磁场，两种变化的场永远互相联系着，形成了统一的电磁场.麦克斯韦提出的位移电流的概念，已为无线电波的发现和它在实际中的广泛应用所证实，它和变化磁场激发电场的概念都是麦克斯韦电磁场理论中很重要的基本概念.根据位移电流的定义，在电场中每一点只要有电位移的变化，就有相应的位移电流密度存在，因此不仅在电介质中，就是在导体中，甚至在真空中也可以产生位移电流，但在通常情况下，电介质中的电流主要是位移电流，传导电流可以略去不计；而在导体中的电流，主要是传导电流，位移电流可以略去不计.至于在高频电流的场合，导体内的位移电流和传导电流同样起作用，这时就不可略去其中任何一个了.

例11.10　如图11.20 所示，半径为R 的两块圆板，构成平板电容器.现均匀充电，使电容器两极板间的电场变化率为dE／dt（常量），求极板间的位移电流以及距轴线r 处的磁感应强度.

解　穿过两极板间任一曲面的电位移通量为

电容器两极板间的位移电流为

图11.20　例11.10 用图

选半径为r 同轴圆周为闭合路径L，由全电流安培环路定理式（11.50）得

又因为

需要注意的是，上述计算得到的磁感应强度都是由传导电流和位移电流共同产生的.