
图11.15 两个线圈的互感
当一个线圈中的电流发生变化时,将在周围空间产生变化的磁场,从而在它附近的另一个线圈中产生感应电动势和感应电流,这种现象称为互感,所产生的感应电动势称为互感电动势.
一个线圈中的互感电动势的大小不仅与另一个线圈中电流改变的快慢有关,而且与两个线圈的结构及它们之间的相对位置有关.
如图11.15 所示,两个相邻的线圈回路1 和2,分别通有电流I1 和I2.根据毕奥⁃萨伐尔定律知,电流I1 产生的磁场B 正比于I1,而它穿过线圈2 的全磁通Ψ21也正比于I1,即
![]()
同理,电流I2 产生的磁场通过线圈1 的全磁通Ψ12为
![]()
式中,M12和M21为比例系数.它们与两个耦合回路的形状、大小、匝数、相对位置以及周围的磁介质情况有关.理论和实验都可以证明,对于给定的一对导体回路,有
![]()
M 值称为两个回路之间的互感系数,简称互感.在国际单位制中,M 的单位也是亨利(H)、毫亨(mH)和微亨(μH).互感一般用实验测得,对一些比较简单的情况也可以计算得到.
根据法拉第电磁感应定律,在互感系数M 一定的条件下,回路中的互感电动势为
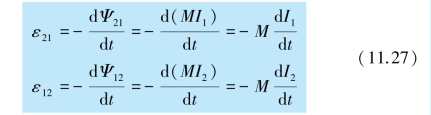
式中,负号表示在一个回路中引起的互感电动势,要反抗另一个回路中的电流变化.当一个回路中的电流随时间变化率一定时,互感越大,则在另一个回路中引起的互感电动势也越大.反之,互感电动势则越小.所以互感是反映两个线圈耦合强弱的物理量.
利用互感可以将一个回路中的电能转换到另一个回路,变压器和互感器都是以此为工作原理的.变压器中有两个匝数不同的线圈,由于互感,当一个线圈两端加上交流电压时,另一个线圈两端将感应出数值不同的电压.互感现象在某些情况下也会带来不利的影响.在电子仪器中,元件之间不希望存在的互感耦合会使仪器工作质量下降甚至无法工作.在这种情况下就要设法减少互感耦合,例如把容易产生不利影响的互感耦合元件远离或调整方向以及采用“磁场屏蔽”措施等.
例11.8 如图11.16 所示,为两个同轴螺线管1 和螺线管2,同绕在一个半径为R 的长磁介质棒上.它们的绕向相同,螺线管1 和螺线管2 的长分别为l1 和l2,单位长度上的匝数分别为n1 和n2,且l1≫R,l2≫R.
(1)试由此特例证明M12 =M21 =M;
(2)求两个线圈的自感L1 和L2 与互感M 之间的关系.

图11.16 例11.8 用图
解 (1)设螺线管1 中通有电流I1,它产生的磁场的磁感应强度大小为
![]()
电流I1 产生的磁场穿过螺线管2 每一匝的磁通量为
![]()
因此有
![]()
结合式(11.25a)可得(https://www.xing528.com)
![]()
式中,V2 =l2πR2 是螺线管2 的体积.
设螺线管2 中通有电流I2,它产生的磁感应强度大小为
![]()
电流I2 产生的磁场穿过螺线管1 每一匝的磁通量为
![]()
由于在长直螺线管的端口以外,B 很快衰减到零,因此螺线管1 中只有n1l2 匝线圈穿过Φ12的磁通量,故I2 的磁场在螺线管1 中产生的总磁通为
![]()
由式(11.25b)可得
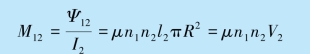
两次计算的互感相等,即证明了
![]()
(2)已计算出长螺线管的自感为L =μn2V,所以
![]()
由此可见
![]()
更普遍的形式为
![]()
式中,k 称为耦合系数,由两个线圈的相对位置决定,它的取值为0≤k≤1.k≪1 时,称为松耦合;当两个线圈垂直放置时,k≈0.
例11.9 一矩形线圈ABCD,长为l,宽为a,匝数为N,放在一长直导线旁边与之共面,如图11.17 所示.这长直导线是一闭合回路的一部分,其他部分离线圈很远,未在图中画出.当矩形线圈中通有电流i=I0 cos ωt 时,求长直导线中的互感电动势.
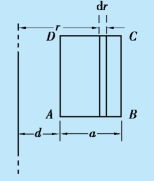
图11.17 例11.9 用图

矩形线圈中的电流i=I0 cos ωt 在长直导线中产生的互感电动势则为

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




