1834 年，俄国科学家E.楞次获悉法拉第发现电磁感应现象后，做了许多实验，在进一步概括了大量实验结果的基础上，得出了确定感应电流方向的法则，称为楞次定律，其具体表述为：在发生电磁感应时，导体闭合回路中产生的感应电流具有确定的方向，总是使感应电流所产生的磁场穿过回路面积的磁通量，去补偿或者反抗引起感应电流的磁通量的变化.
在图11.6 的实验中，当磁铁棒以N 极插向线圈或线圈向磁棒的N 极运动时，通过线圈的磁通量增加，感应电流所激发的磁场方向则要使通过线圈面积的磁通量反抗线圈内磁通量的增加，所以线圈中感应电流所产生的磁感应线的方向与磁铁棒的磁感应线的方向相反.再根据右手螺旋定则，可确定线圈中感应电流的方向.如图11.6（a）中的箭头所示，当磁铁棒拉离线圈或线圈背离N极运动时，通过线圈面积的磁通量减少，感应电流的磁场则要使通过线圈面积的磁通量去补偿线圈内磁通量的减少，因此，它所产生的磁感应线的方向与磁铁棒的磁感应线的方向相同，感应电流的方向应如图11.6（b）中箭头所示.
楞次定律实质上是能量守恒定律的一种体现.在上述例子中可以看到，当磁铁棒的N 极向线圈运动时，线圈中感应电流所激发的磁场分布相当于在线圈朝向磁铁棒一面出现N 极，它阻碍磁铁棒的相对运动，因此，在磁铁棒向前运动过程中，外力必须克服斥力做功；当磁铁棒背离线圈运动时，则外力必须克服引力做功，在这个过程中，线圈中感应电流的电能将转化为电路中的焦耳⁃楞次热.反过来，如果设想感应电流的方向不是这样，它的出现不是阻碍磁铁棒的运动而是促使它加速运动，那么只要我们把磁铁棒稍稍推动一下，线圈中出现的感应电流将使它动得更快，于是又增长了感应电流，这个增长又促进相对运动更快，如此不断地相互反复加强，于是只要在最初使磁铁棒的微小移动中做出很小的功，就能获得极大的机械能和电能，这显然是违背能量守恒定律的.
所以，感应电流的方向遵从楞次定律的事实表明，楞次定律本质上就是能量守恒定律在电磁感应现象中的具体表现.因此楞次定律还有另外一种表述方式，即在闭合导体回路中，感应电流总是企图产生一个磁场去阻碍穿过该回路所围面积的磁通的变化.
图11.6 楞次定律
例11.2 如图11.7 所示，一长直电流I 旁距离为r 处有一与电流共面的圆线圈，线圈的半径为R，且R≪r.就下列两种情况求线圈中的感应电动势.
图11.7 例11.2用图
（2）若线圈以速率v 向右平移.
解 因为R≪r，所以线圈所在处磁场可看成均匀的，有
且方向垂直线圈平面向里，故穿过线圈平面的磁通量为
（1）按法拉第电磁感应定律，线圈中的感应电动势大小为
由楞次定律可知，感应电动势为逆时针方向.
（2）按法拉第电磁感应定律
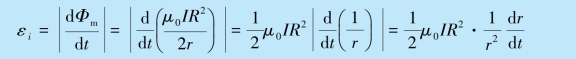(www.xing528.com)
由楞次定律可知，感应电动势为顺时针方向.
例11.3 如图11.8 所示，在均匀磁场B 中有N 匝面积为S 且可绕轴OO′转动的线圈并排放在一起.若线圈以恒定角速度ω 转动，求线圈中产生的感应电动势的大小.
解 假设在t ＝0 时刻线圈法向单位矢量en 与磁场方向一致，则在某时刻t，en 与B 的方向间的夹角为θ ＝ωt.此时穿过N 匝线圈的磁链为
根据式（11.1），产生的感应电动势为
图11.8 例11.3 用图
令NBSω＝εm，上式变为其中f＝ω／2π 为线圈单位时间转动的圈数，即频率.
由以上结果可以清楚地看出，磁场中匀速转动的线圈产生的感应电动势是时间的正弦函数.其中的εm 叫做感应电动势的最大值，也称为振幅，如图11.9（a）所示.
当外电路中接有电阻R 时，由欧姆定律可知回路中产生的感应电流为
其中Im 为感应电流的最大值.
可见，此时产生的感应电流也是时间的正弦函数，如图11.9（b）所示.这种电流就是我们平时所说的正弦交变电流，简称交流电（alternating current）.现实中的交流发电机就是基于以上原理制成的.
图11.9 感应电流
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
