有磁介质时的高斯定理和安培环路定理 《大学物理学》

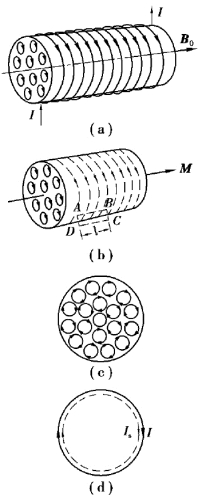
图10.23　磁化电流

1）磁化电流

在磁化状态下，由于分子电流的有序排列，磁介质中将出现宏观电流.以顺磁质为例，如图10.23 所示，当介质磁化后，各分子磁矩沿外磁场方向排列，分子电流与分子磁矩的方向成右手螺旋关系.在介质内部，相邻分子电流的方向彼此相反，相互抵消；在介质表面附近的薄层内，分子电流靠近介质内部的部分被抵消，只有在介质截面边缘各点上分子电流的效应未被抵消，它们在宏观上形成了与截面边缘重合的一种看似由一段段分子电流连续接成的等效大圆形电流，这一等效电流称为磁化电流，又称束缚电流.

磁化电流不同于前面学过的传导电流，它实质上是分子电流，受到每个分子的约束，它的产生不伴随电荷的宏观位移.尽管两种电流在产生机制和热效应方面存在区别，但在激发磁场和受磁场作用方面却是完全等效的.

2）有磁介质时的高斯定理

磁介质在外磁场中会发生磁化，同时产生磁化电流Is，因此磁介质内部的磁场B 是外磁场B0 和磁化电流Is 所激发的磁场B′的矢量和.由于磁化电流在激发磁场方面与传导电流相同，它们所激发的磁场均由真空中的毕奥⁃萨伐尔定律决定，都是涡旋场，因此在有磁介质时磁场中的高斯定理仍然成立，即

式（10.75）就是普遍情况下的高斯定理.在真空中，磁场B 即为外磁场；在磁介质中，磁场B 是外磁场B0 和磁化电流Is 所激发的磁场B′的矢量和.

3）有磁介质时的安培环路定理

圆柱体磁介质表面上沿柱体母线方向单位长度的磁化电流，称为磁化电流面密度Js.在长为L、横截面为S 的磁介质里，由于被磁化而具有的磁矩值为∑m ＝JsLS，于是由式（10.74）可得磁化电流面密度和磁化强度之间的关系为

若在如图10.23（b）所示的圆柱体磁介质内外横跨边缘处选择ABCDA 矩形环路，并设AB ＝l，那么磁化强度M 沿此环路的积分为

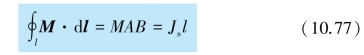
同时，对ABCDA 环路来说，由安培环路定理可有

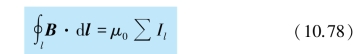
式中，∑Il 既包含传导电流∑I，又包含磁化电流∑Is ＝Jsl，于是可将上式改写为

将式（10.77）与上式结合，有

整理后即

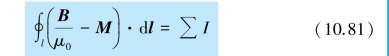
引入辅助矢量H，H 称为磁场强度，其定义为

由此得

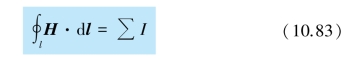
式（10.83）就是有磁介质时的安培环路定理，即磁场强度沿任意闭合回路的线积分（即H 的环流），等于该回路所包围的传导电流的代数和.由该定理可知，H 的环流与磁化电流无关，因此引入H 矢量后，在磁场及磁介质的分布具有某些对称性时，可以根据传导电流的分布求出H 的分布，再由磁感应强度与磁场强度的关系求出B 的分布.在国际单位制中，磁场强度H 的单位是安培每米，符号是A／m.

式（10.82）表明了磁介质中任意一点的磁感应强度B、磁场强度H 和磁化强度M 三者之间的普遍关系，不论磁介质是否均匀，甚至对铁磁质都能适用，通常写成

显然，磁化强度M 不仅和磁介质的性质有关，也和磁介质所在处的磁场有关.实验证明，在弱磁性物质的磁场内，任一点的磁化强度M 与磁场强度H 之间有如下关系：

式中，比例系数χm 只与磁介质的性质有关，称为磁介质的磁化率.因为磁化强度M 与磁场强度H 单位相同，所以磁介质的磁化率χm 的量纲为1.

利用式（10.85）可以将式（10.84）改写为

令

因此磁介质中的磁感应强度可以写成(www.xing528.com)

式中，μ＝μ0μr，称为磁介质的磁导率.

对于真空中的磁场，磁化强度M ＝0，磁感应强度B ＝μ0H，这表明真空相当于相对磁导率μr ＝1 的“磁介质”；对于顺磁质，磁化率χm＞0，所以相对磁导率μr＞1；对于抗磁质，磁化率χm＜0，所以相对磁导率μr＜1.

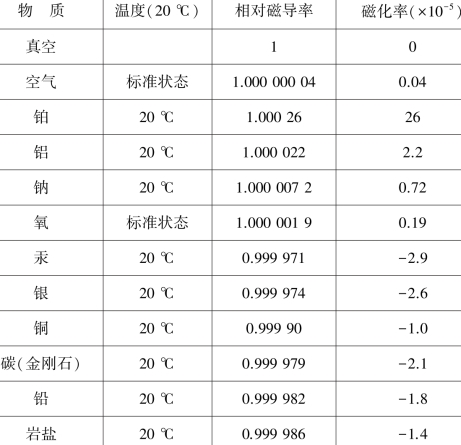
常见物质的相对磁导率和磁化率如表10.1 所示.

表10.1　常见物质的相对磁导率和磁化率

例10.10　如图10.24 所示，半径为R1 的无限长圆柱体导线外有一层同轴圆筒状均匀磁介质，其相对磁导率为μr，圆筒外半径为R2，设电流I 在导线中均匀流过.试求：

（1）导线内的磁场分布；

（2）磁介质中的磁场分布；

（3）磁介质外面的磁场分布.

取导线的磁导率为μ0.

解　圆柱体电流所产生的磁感应强度B 和磁场强度H 的分布均具有轴对称性.设a、b、c 分别为导线内、磁介质中及磁介质外的任一点，它们到圆柱体轴线的垂直距离用r 表示，取以r 为半径的圆周的闭合回路，如图10.24 所示.

（1）对过a 点的闭合回路，应用磁介质中的安培环路定理，得

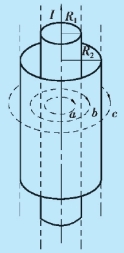
图10.24　例10.10 用图

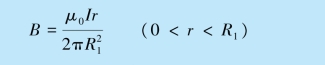
（2）对过b 点的闭合回路，应用磁介质中的安培环路定理得

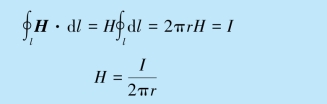
由此得磁介质中的磁感应强度为

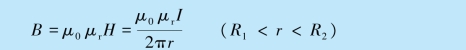
（3）将磁介质中的安培环路定理应用于过c 点的闭合回路，仍然有

于是得磁介质外面的磁感应强度为

再由B＝μH（导线内的磁导率μ＝μ0），得导线内的磁感应强度为

磁感应强度B 和磁场强度H 的方向均与电流成右手螺旋关系.

根据以上讨论可见，整个磁场中，磁场强度H 是连续的，而在不同介质的界面处，磁感应强度B 是不连续的，存在着突变.

例10.11　如图10.25 所示，在密绕螺绕环内充满均匀磁介质，已知螺绕环上线圈总匝数为N，通有电流I，环的横截面半径远小于环的平均半径，磁介质的相对磁导率为μr.求磁介质中的磁感应强度.

解　由于电流和磁介质的分布对环的中心具有轴对称性，所以与螺绕环共轴的圆周上各点的磁场强度H 大小相等，方向沿圆周的切线.在环管内取与环共轴的半径为r 的圆周为安培环路，应用磁介质中的安培环路定理得

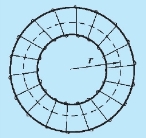
图10.25　例10.11 用图

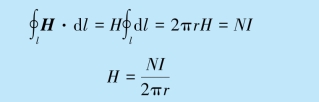
再由B＝μH，得环管内的磁感应强度为

磁感应强度B 和磁场强度H 的方向均与电流成右手螺旋关系.