霍尔效应-大学物理学

如图10.21 所示，将一块宽度为b、厚度为d 的导电板放在磁感应强度为B 的磁场中，并在导电板中通以纵向电流I，此时在板的横向两侧面A、A′之间呈现出一定的电势差UH.这一现象称为霍尔效应（Hall effect），所产生的电势差UH 称霍尔电压.实验表明，霍尔电压的值为

其中比例系数RH 称为霍尔系数.

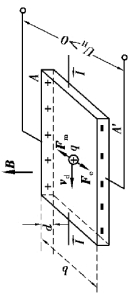
图10.21　霍尔效应示意图

霍尔效应可以用带电粒子在电磁场中的运动来解释.导体板上的电流是带电粒子的定向运动而成，以带正电粒子为例，则其运动方向与电流方向相同.如图10.21 所示，设导体板中的载流子为电荷q，漂移速度为vd.于是载流子在磁场中要受洛伦兹力Fm的作用，其大小为Fm ＝qvB.在洛伦兹力的作用下，导体板内的载流子将向板A 移动，从而使A、A′两侧面上分别有正、负电荷的积累.这样，便在A、A′之间建立起电场强度为E 的电场，于是载流子就要受到一个与洛伦兹力方向相反的电场力Fe.随着A、A′两侧面上电荷的积累，Fe 也不断增大.当电场力增大到正好等于洛伦兹力时，即Fe ＝Fm，电荷将不再继续积累，达到了动态平衡.这时，导体板A、A′两侧面之间的横向电场称为霍尔电场EH，此时它与霍尔电压UH 之间的关系为

由于动态平衡时电场力与洛伦兹力相等，有

于是

上式给出了霍尔电压UH，磁感应强度B 以及载流子漂移速度vd 之间的关系.考虑到漂移速率vd 与电流I 的关系，有

所以可将式（10.66）改写，得霍尔电压为

(www.xing528.com)

对于一定材料，载流子数密度n 和电荷q 都是一定的.式（10.68）与式（10.63）相比较，可得霍尔系数的理论值为

可见霍尔系数RH 与载流子数密度n 成反比.应该注意：从霍尔电压的正负，可以判断载流子带的是正电还是负电；载流子数密度n 越小，霍尔系数RH 越大，霍尔效应越明显.我们知道，在金属导体中，由于自由电子数密度很大，故金属导体的霍尔系数很小，相应的霍尔电压也很弱.在半导体中，载流子数密度要低得多，因此半导体的霍尔系数比金属导体大得多，所以半导体能产生很强的霍尔效应.

霍尔效应目前在科研、生产中已有广泛的应用.例如利用霍尔电势差来测定磁感应强度B、电流、血流等.

另外，我们从式（10.68）中可以看出，在给定电流I 和导体厚度d 情况下，霍尔电压随磁感强度B 的增加而线性地增加.然而，1980 年德国物理学家克利青（K.Klitzing，1943—），在研究低温和强磁场下半导体的霍尔效应时，发现霍尔电压UH 与B 的关系如图10.22 所示.从图中可以看出UH 与B 之间的关系不再是线性的，而是出现了一系列的“台阶”.这一效应称为量子霍尔效应（quantum Hall effect）.相应的霍尔电阻为

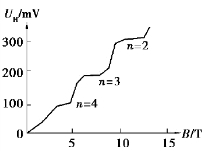
图10.22　霍尔电压UH 与B 的关系图

式中，h 为普朗克常量，e 为元电荷，它们的值可以由物理常量表查得.按照量子霍尔效应理论，所以霍尔电阻为

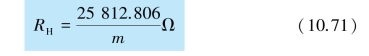
m＝1 时的霍尔电阻为25 812.806 Ω.由于量子霍尔效应给电阻提供了一个新的测量基准，其精度可达10－10.所以1990 年人们把由量子霍尔效应所确定的电阻25 812.806 Ω 作为标准电阻.为了表彰克利青发现了量子霍尔效应，他于1985 年获诺贝尔物理学奖.随后，美籍华裔物理学家崔琦（D.C.Tsui， 1939—）等于1982年在研究更强磁场中的量子霍尔效应时发现了分数量子霍尔效应（fractional quantum Hall effect），并以此获得了1998 年的诺贝尔物理学奖.