安培最早发现两条静止载流导线之间存在相互作用力,并把每一导线所受的力解释为另一导线对它的磁力.人们把磁场对载流导体的磁力作用称为安培力.安培总结出了载流回路中一段电流元在磁场中受力的基本规律:磁场对电流元Idl 的作用力dF,在数值上等于电流元的大小、电流元所在处磁感应强度B 的大小,以及电流元与磁感应强度两者方向间夹角θ 的正弦之乘积,其数学表达式为
![]()
dF 的方向服从右手螺旋法则,写成矢量形式为
![]()
式(10.54)、式(10.55)称为安培定律.
对任意形状的载流导线L,其在磁场中所受的安培力F 等于各个电流元所受安培力dF 的矢量和,即
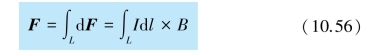
一般情况下,在计算一段载流导线的安培力时,如果各电流元所受磁场力的方向是一致的,则上式积分就转化成标量积分.特别地,对均匀磁场中的一条通有电流I、长为L 的直导线,电流方向与磁场B 方向的夹角为θ,导线受到的安培力为
![]()
当θ=0°或180°时,F =0;当θ=90°时,F =Fmax =ILB.
后来人们认识到导线中的电流是带电粒子的定向运动,而运动的带电粒子在磁场中要受洛伦兹力,这两者的结合给出了载流导线在磁场中所受磁力(安培力)的本质:在洛伦兹力Fm =qv×B的作用下,导体内做定向运动的电子和导体中晶格处的正离子不断碰撞,从而将动量传给了导体,进而使整个载流导体在磁场中受到磁力的作用,这就是安培力.由此可见,安培力是洛伦兹力的一种宏观表现,因此可以从洛伦兹力公式出发得到静止载流导线的安培力公式(10.54)、(10.55),不过此处不再做相关介绍,读者不妨自行推导.
例10.9 如图10.18 所示,在均匀磁场中放置一任意形状的导线,电流为I,求此段载流导线所受的安培力.
解 在载流导线上任取电流元Idl,它受到的安培力为
![]()
写成分量的形式,有
![]()
因此整个导线受力为(https://www.xing528.com)
![]()
相当于载流直导线OP 在均匀磁场中受的力,方向沿y 方向.
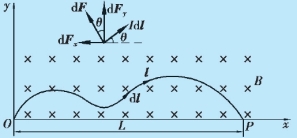
图10.18 例10.9 用图

图10.19 电流单位“安培”的定义
如图10.19 所示,两平行无限长直导线AB、CD 相距为a,分别通有电流I1、I2,它们之间会有相互作用力.导线CD 的任一电流元I2dl2 处于电流I1 激发的磁场中,
![]()
电流元I2dl2 所受的安培力为

方向垂直于CD 指向AB.所以导线CD 上单位长度所受的安培力为

同理,导线AB 上单位长度所受的安培力为

方向垂直于AB 指向CD.容易看出两导线AB、CD 之间的作用力是相互吸引力.不难证明,当两导线中通以方向相反的电流时,两导线之间的作用力是相互排斥力.由于两导线间的相互作用力比较容易测量,所以在国际单位制中正是通过两平行载流直导线的作用力来定义电流的单位:在真空中两根截面积可略去的平行长直导线,二者之间相距1 m,通以流向相同、大小等量的电流时,调节导线中电流的大小,使得两导线间每单位长度的相互吸引力为2×10-7 N/m,则规定此时每根导线中的电流为1 A,称为1 安培.根据“安培”的定义,还可以计算出真空磁导率的数值为μ0 =4π×10-7 N/A2.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




