磁场对运动电荷的作用

带电粒子运动方向平行（或反平行）磁场方向时，它受到的磁场力为零；当带电粒子运动方向垂直于磁场方向时，它受到的磁场力最强，其值为

且Fm 与粒子运动速度v 和磁感应强度B 相互垂直.

一般情况下，当带电粒子的运动方向与磁场方向夹角为θ，则所受磁场力F 的大小为

而F 的方向垂直于v 和B 决定的平面，并与qv 和B 的方向成右手螺旋关系，即右手四指由qv 的方向（q＞0 时即v 的方向；q＜0 时为v 的反方向）经小于π 的角度转向B 的方向时大拇指所指的方向，故其矢量表达式为

式（10.45）就是磁场对运动电荷的作用力，即洛伦兹力的公式.

洛伦兹力总是和电荷速度方向垂直，因此磁力只改变电荷的运动方向，而不改变其速度的大小和动能.洛伦兹力对电荷所做的功恒等于零，这是洛伦兹力的一个重要特征.下面分三种情况讨论带电粒子在均匀磁场中的运动：

（1）带电粒子q 以速率v0 沿磁场B 方向进入均匀磁场.由式（10.45）可知，粒子不受磁场力的作用，它将沿着磁场B 方向做匀速直线运动.

（2）带电粒子q 以速率v0 沿垂直于磁场B 方向进入均匀磁场.由式（10.45）可知，粒子受到洛伦兹力的作用，大小为F ＝qv0B.因为洛伦兹力始终与速度方向垂直，所以带电粒子的速度大小不变，只改变方向.带电粒子将作半径为R 的匀速圆周运动，洛伦兹力提供向心力，因此有

由此得带电粒子的轨道半径为

由式（10.47）可知，对于一定的带电粒子（即q／m 一定），其轨道半径与带电粒子的运动速度成正比，而与磁感应强度成反比；速度越小，洛伦兹力和轨道半径也越小.

带电粒子运动一周所需的时间（即周期）为

单位时间内带电粒子的绕行圈数称为回旋频率，它是周期的倒数.(www.xing528.com)

（3）带电粒子q 以速度v0 与磁场B 成θ 夹角进入均匀磁场将速度v0 分解成平行于磁场B 的分量v／ ／和垂直于磁场B 的分量v⊥，有

带电粒子同时参与两种运动，一种是平行于磁场的匀速直线运动，速度为v／ ／；另一种是在垂直于磁场方向以速率为v⊥作匀速圆周运动，轨道半径R 为

周期T 为

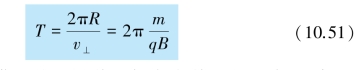
一个周期内，带电粒子沿着磁场方向前进的距离，即螺距h 为

综上所述，带电粒子的合运动是以磁场方向为轴的等螺距的螺旋运动.如图10.16 所示，一束发散角不大的带电粒子束，当它们在磁场B 的方向上具有大致相同的速度分量时，它们有相同的螺距h.经过一个周期它们将重新会聚在另一点，这种发散粒子束会聚到一点的现象与透镜将光束聚焦现象十分相似，因此称为磁聚焦.带电粒子在磁场中作螺旋线运动的轨道半径R 与磁感应强度成反比，磁场越强， 轨道半径R 越小.在很强的磁场中，每个带电粒子的活动便被约束在一根磁场线附近的很小范围内作螺旋线运动，运动的中心只能沿磁场线作纵向移动，一般不能横越它.因此强磁场可以使带电粒子的横向运动受到很大的限制，这种能约束带电粒子运动的磁作用效应称为磁约束.

图10.16　磁聚焦

在既有电场又有磁场的情况下，运动的带电粒子q 在此区域内所受到的作用力应是电场力与磁场力的矢量和，即作用在带电粒子上的力应为

式（10.53）通常也被称为洛伦兹力公式.利用外加的电场和磁场来控制带电粒子流的运动，这在近代科学技术中的应用是极为重要的.

加速器是提供高能粒子的主要实验装置，加速器输出粒子的能量称为加速器的能量，劳伦斯率先于1930 年提出了回旋加速器方案.回旋加速器的基本思想是用磁场把带电粒子的运动限制在某一空间范围，再用较小的电场使之多次加速.如图10.17 所示，将两个空心的半圆形铜盒D1、D2 留有间隙地放在电磁铁的两个磁极之间，盒内空间便充满与盒面垂直的均匀恒定磁场.将两盒分别连接电源两极，间隙处便有电场.由于屏蔽作用，两盒内部电场均为零.带电粒子以某一初速垂直进入第一个半圆形铜盒后，在磁场力作用下作匀速圆周运动，转过半圈后进入间隙，受到间隙处的电场加速然后进入第二个半圆形铜盒.由式（10.50）可知带电粒子以较大半径作匀速圆周运动，转过半圈后再次进入间隙.如果此时电场反向，则带电粒子会再次受到电场加速后返回第一个半圆形铜盒.如此反复，则带电粒子多次受到电场的加速，能量越来越高，直至从铜盒边缘引出.由式（10.51）还可知，在不考虑相对论效应的情况下，带电粒子在铜盒中作半个圆周运动所需要的时间只与带电粒子的电荷q、质量m 以及磁感应强度B 有关，与带电粒子的速度或能量没有关系.

图10.17　回旋加速器