在静电学中,当电荷分布有某些对称性时,单从高斯定理就可求得静电场.类似地,在静磁学中,当电流分布有某些对称性时,单从安培环路定理就可求得恒定磁场.
例10.6 求无限长载流圆柱导体的磁场.
解 设圆柱半径为R,电流I 沿轴线方向均匀流过横截面.由电流分布沿轴线的平移对称性可知磁感应强度B 也有这种对称性.因此只需讨论任一与轴垂直的平面内的情况.磁场对圆柱轴线具有旋转对称性,所以磁感应线应该是在垂直轴线的平面内、以轴线为中心的一系列同心圆,方向与其内部的电流成右手螺旋关系,而且在同一圆周上磁感应强度的大小相等,如图10.13 所示.
过任一场点P,在垂直轴线的平面内取中心在轴线上、半径为r 的圆周为积分路径L,积分方向与磁感应线的方向相同.由于L 上磁感应强度的量值处处相等,且磁感应强度B 的方向与积分路径dl 的方向一致,所以,磁感应强度B 沿路径L 的环流为

图10.13 例10.6 用图
![]()
如果点P 为圆柱体内任意一点,即r<R,因为圆柱体内的电流只有一部分I′通过环路.由安培环路定理得
![]()
由于电流I 均匀分布,所以
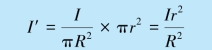
上面两式联立得
![]()
如果点P 为圆柱体外任意一点,即r>R,由安培环路定理得

所以
![]()
这与无限长载流直导线的磁场分布完全相同.
例10.7 求无限长直载流螺线管的磁场.
解 如图10.14 所示,设无限长载流螺线管单位长度上绕有n 匝线圈,现通有电流I.每匝线圈都会在其周围产生载流圆环磁场,当线圈彼此挨近形成无限长螺线管时,在螺线管外,磁场倾向于抵消;在螺线管内,磁场得到加强.进一步根据电流分布的对称性分析,可确定螺线管内的磁感应线是一系列与轴线平行的直线,而且在同一磁感应线上各点的磁感应强度大小相同.
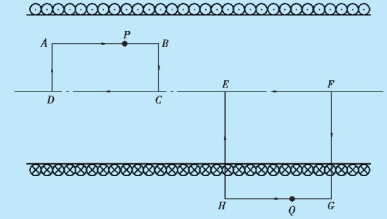
图10.14 例10.7 用图
首先求管内任一点P(不在轴线上)的B.为此作一闭合矩形环路ABCD,其中AB 边过P 点,CD 边在轴线上,前面已计算得到螺线管轴线上磁感应强度大小B =μ0nI,方向水平向右;根据对称性讨论,可以证明AB 段B 大小相等,方向水平向右;而BC、DA 两段上B处处向右,与dl 处处垂直;且闭合环路ABCD 内不包围电流,因此对该环路应用安培环路定理,则有

由此可以看到,管内任一点的磁感应强度与轴线上相同,表明管内是均匀磁场.(https://www.xing528.com)
再求管外任一点Q 的B.作闭合矩形回路EFGH,其中GH 边过Q 点,EF 边在轴线上.对该闭合回路应用安培环路定理,注意到环路包围的电流为nI·EF,则

所以
![]()
因此
![]()
即管外磁感应强度处处为零,磁场集中在管内.
由于矩形回路是任取的,不论AB 边在管内任何位置,式(10.42)都成立.因此,无限长直螺线管内任意一点的磁感应强度B 的大小相同,方向平行于轴线,即细螺线管内中间部分是均匀磁场,细螺线管外磁感应强度为零.
例10.8 求载流螺绕环的磁场.
解 如图10.15(a)所示的环状螺线管称为螺绕环.设真空中有一螺绕环,环的平均半径为R,环上均匀地密绕N 匝线圈,线圈通有电流I,求载流螺绕环的磁场.由电流的对称性可知,环内的磁感应线是一系列同心圆,圆心在通过环心垂直于环面的直线上.在同一条磁感应线上各点磁感应强度的大小相等,方向沿圆周的切线方向,与圆内电流成右手螺旋关系.

图10.15 例10.8 用图
先分析螺绕环内任意一点P 的磁场,以环心为圆心、过P 点作一闭合环路L,半径为r,绕行方向与所包围电流成右手螺旋关系,如图10.15(b)所示.则由安培环路定理得
![]()
计算出P 点磁感应强度为
![]()
如果环管截面半径比环半径小得多,可以认为r≈R,则上式可以写成
![]()

对螺绕环外任意一点的磁场:过所求场点作一圆形闭合环路,并使它与螺绕环共轴.很容易看出,穿过闭合回路的总电流为零,因此根据安培环路定理
![]()
得
![]()
所以,对密绕细螺绕环来说,它的磁场几乎全部集中在螺绕环的内部,外部无磁场;环内的磁场可视为均匀的,方向由右手螺旋法则确定.从物理实质上来说,这样的螺绕环等同于无限长直螺线管.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




