大学物理学：电容器的电容

两个带有等值而异号电荷的导体所组成的带电系统称为电容器，这两个导体称为电容器的两个极板.电容器可以储存电荷，以后将看到电容器也可以储存能量.如图9.44 所示，两个导体A、B 放在真空中，它们所带的电量分别为＋q、－q，如果A、B 的电势分别为VA、VB，那么A、B 之间的电势差为VA－VB，电容器的电容定义为

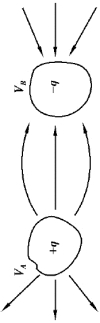
图9.44　导体A 和导体B 组成一电容器

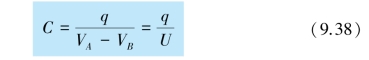
利用电容的定义式（9.38），我们可以推得孤立导体的电容.如将B 移至无限远处，则VB ＝0.所以，孤立导体的电量q 与其电势V之比称为孤立导体的电容，用C 表示，记作

电容的单位为法拉，简称法（F），1 F＝1 C／1 V.实用中法拉这个单位较大，故常用微法（μF）或皮法（pF），它们之间的换算关系为

电容器是重要的电路元件，通常由两块靠得很近的、中间充满电介质的金属平板构成.电容器的种类很多，按大小分，有比人还高的巨型电容器，也有肉眼无法看到的微型电容器；根据内部介质不同可分为空气的、蜡纸的、云母的、涤纶薄膜的、陶瓷的电容器等；按形状可分为球形电容器、平行板电容器、圆柱形电容器等.

例9.16　计算平行板电容器的电容.

图9.45　例9.16 用图

于是极板间的电势差为

(www.xing528.com)

由电容器电容的定义式，可得平行板电容器的电容为

由式（9.40）看出，平行板电容器的电容与极板面积S 成正比，与板间距离d 成反比，与电介质的相对电容率εr 成正比，与极板电荷无关.

例9.17　计算球形电容器的电容.

解　球形电容器是由两个同心的金属导体球壳组成.内球壳半径为RA，外球壳半径为RB，所带电荷分别为q 和－q，两球壳间充满相对电容率为εr 的电介质，如图9.46 所示.由有电介质时的高斯定理，求得两球壳之间的电场强度为

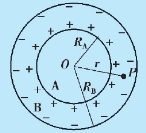
图9.46　例9.17 用图

则两球壳之间的电势差为

根据电容器电容的定义式有

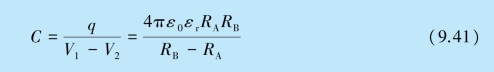
式（9.41）即为球形电容器的电容公式.