电势梯度及等势面的绘制方法

1）等势面

前面曾用电场线来描绘电场中各点的场强，现在，也可用绘图方法来描绘电场中各点的电势，从而更形象地研究电势与场强之间的关系.

一般说来，电场中各点的电势不同，但电场中也有许多点的电势相等.我们把电场中电势相等的点所组成的曲面叫等势面.与电场线的画法一样，对等势面的画法也有规定：电场中任意两个相邻的等势面之间的电势差都相等.图9.21 所示的几种典型电场的等势面就是按此规定画出的，图中带箭头的线表示电场线、不带箭头的线表示等势面.

等势面具有以下特点：

（1）在同一等势面上的任意两点间移动电荷，电场力不做功.

设a、b 为等势面上的任意两点，如图9.22 所示.若移动电荷q从a 到b，因为Va ＝Vb，所以Aab ＝q（Va－Vb）＝0.这是因为等势面上各点的电势相等，电荷在同一等势面上各点具有相同的电势能，所以在同一等势面上移动电荷时，其电势能不变，即电场力不做功.

（2）等势面一定与电场线垂直，即与场强的方向垂直.

设试验电荷沿某等势面有一微小位移dl，这时，虽然电场对试验电荷有力的作用，但根据等势面的定义，电场力所做的功为零.即dA＝qE·dl＝qE cos θdl ＝0，因为q、E、dl 都不等于零，所以只有cos θ ＝0，即θ ＝π／2.也就是说，试验电荷在等势面上任一点所受的电场力总是与等势面垂直，亦即电场线的方向总是与等势面垂直.

（3）电场线总是由电势较高的等势面指向电势较低的等势面.

（4）等势面密集处的电场强度大，等势面稀疏处电场强度小.从等势面的疏密程度可以比较出场强的强弱.

利用等势面既可以形象地描述电场的性质，也可由等势面来绘制电场线.由于实际中测定电势差比测定电场要容易得多，因此常用等势面来研究电场，即先描绘出等势面的形状和分布，再根据电场线与等势面之间的关系描绘出电场线的分布.

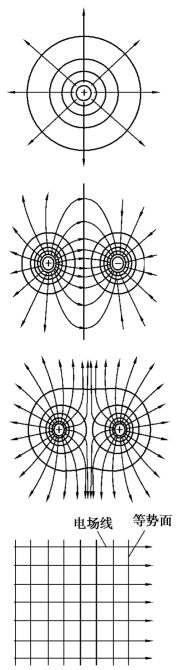
图9.21　几种常见电场的等势面和电场线图

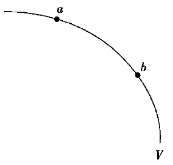
图9.22　等势面

2）电势梯度

如图9.23 所示，在电场中任取两相距很近的等势面1 和2，电势分别为V 和V＋dV，且dV ＞0.电势为V 的等势面上a 点的单位法向矢量为en，与电势为V＋dV 的等势面正交于一点c.在电势为V＋dV 的等势面上任取一点b，设a 到电势为V＋dV 的等势面的法向距离为dn， a 到b 的距离为dl，由图可知，

图9.23　场强与电势梯度

可得

从上式可知，电场中某点的电势梯度，在方向上与该点处电势增加率最大的方向相同，在量值上等于沿该方向上的电势增加率.

3）电场强度和电势梯度的关系

当等势面1 与等势面2 间距离足够小时，两等势面间的电场可看作匀强电场，电荷q 从等势面1 移动到等势面2，电场力做功

因为电场力做功等于电势能的减少量，即

由以上两式联立可得

由此可见，场强也与等势面垂直，但指向电势降低的方向.将上式写成矢量形式有

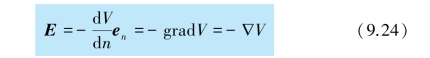
这就是场强和电势梯度的关系，它说明静电场中各点的电场强度等于该点电势梯度的负值.

在直角坐标系中，

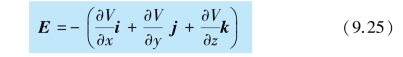
可以看出：

（1）电场强度的方向是电势降落最快的方向；电场强度的大小表示电势沿这个方向上的最大空间减少率.因此电场强度等于电势梯度的负值，其负号表示电场强度的方向与电势梯度的方向相反，即指向电势降低的方向.

（2）在电势等于常数（或为零）的地方，场强不一定为零，只有在电势不变的区域，场强才为零.同样地，在场强为零处，电势不一定为零.

例9.10　求电偶极子所产生的静电场中任意一点的电势.

解　在电偶极子所产生的电场中任取一点P，该点到正、负电荷的距离分别为r＋和r－，P 点到电偶极子中心的距离为r，建立如图9.24 所示坐标系.＋q 和－q 单独存在时，在P点产生的电势分别为

根据电势叠加原理，电偶极子在P 点产生的电势为(www.xing528.com)

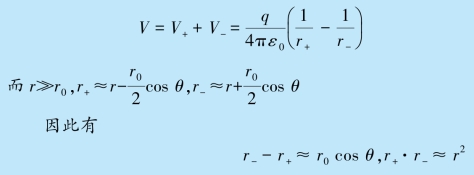
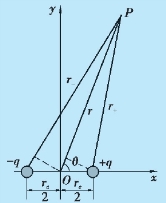
图9.24　例9.10 用图

则有

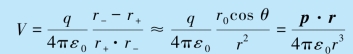
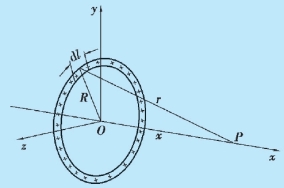
图9.25　例9.11 用图

例9.11　求均匀带电细圆环轴线上任意一点的电势.

根据电势叠加原理，P 点的电势为

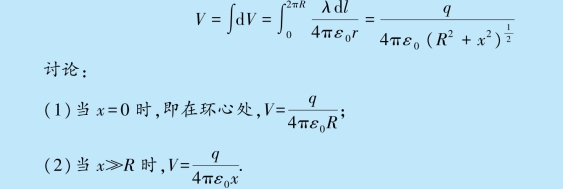
例9.12　如图9.26 所示，两个均匀带电的同心球面，半径分别为R1 和R2，带电量分别为q1 和q2.求场强和电势的分布.

解　（1）对称性分析：①场强沿径向；②离球心O 距离相等处，场强的大小相同.可见场强具有球对称性，可以用高斯定理求场强.

（2）选择高斯面：选与带电球面同心的球面作为高斯面.

当r＞R2 时，取半径为r 的高斯面S1，由高斯定理得

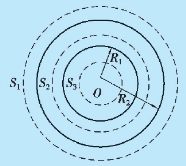
图9.26　例9.12 用图

因为场有上述的对称性，所以

解得

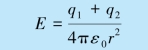
当R1＜r＜R2 时，取半径为r 的高斯面S2，由高斯定理得

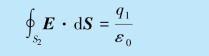
因场强有球对称性，故解出

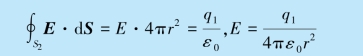
当r＜R1 时，取半径为r 的高斯面S3，因∑q ＝0，故由高斯定理得

所以

从上面计算的结果得到场强的分布为

知道了场强分布，便可以从电势的定义出发求出空间的电势分布：

当r＞R2 时

当R1＜r＜R2 时

当r＜R1 时

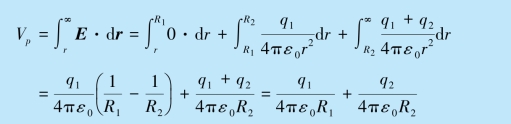
当然，本题也可以用电势叠加原理来求电势的分布，把空间各点的电势看作两个带电球面在空间产生的电势的叠加，求得的结果和利用高斯定理、从电势定义出发求得的结果相同（读者可自己计算验证）.