大学物理学：电场强度叠加

1）电场

任何物体之间的作用力都是靠中间媒质传递的，电荷也不例外.这就说明电荷周围必然存在一种特殊物质，尽管看不到摸不着，但确实存在，是物质存在的一种形态，这种特殊物质称为电场.任何电荷在空间都要激发电场，电荷间的相互作用是通过空间的电场传递的，电场对处于其中的其他电荷有力的作用.若电荷相对于惯性参考系是静止的，则在它周围所激发的电场是不随时间变化的电场，称为静电场.

2）电场强度

电场是一种不能被人们直接感知的物质，为了表示和研究电场中各点的性质，从电场对电荷有作用力这种特性出发，引入试验电荷q0，试验电荷满足如下要求：

（1）试验电荷q0 必须是点电荷；

（2）它所带电荷量也必须足够小，以便把它放入电场后，不会对原有的电场构成影响.

实验表明，在电场中给定点处，试验电荷q0 所受到电场力F的大小和方向是确定的；但在电场中的不同点，如图9.5 所示，q0所受电场力F 的大小和方向一般不同；而且在电场中同一位置，q0 所受电场力F 的大小和方向随q0 而变化，但无论q0 如何变化，其所受电场力F 与其电荷量q0 的比值始终保持不变.可见F／q0与试验电荷q0 无关，它反映的是电场中某点的性质.因此，可以把F／q0 作为描述电场性质的物理量，称为电场强度，简称场强，用E表示.即

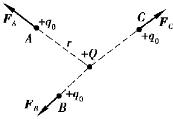
图9.5　不同位置的试验电荷的受力情况

如果q0 ＝1 C，则E 与F 数值相等，方向相同.可见，电场中某点的电场强度在量值上等于单位正电荷在该点所受的电场力的大小，其方向就是正电荷在该点所受的电场力的方向.在国际单位制中，场强的单位是牛／库（N／C）或伏／米（V／m）.

3）点电荷的电场强度

根据电场强度E 的定义，计算点电荷Q 所产生的电场的场强分布.结合图9.5，在真空中有一个点电荷Q，则在其周围电场中，距离Q 为r 的A 点处置一试验电荷q0，则作用于q0 的电场力为

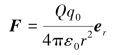
式中，er ＝r／r 是从点电荷Q 到A 点的位置矢量方向的单位矢量，r表示从点电荷Q 到A 点的位置矢量（矢径）.根据场强定义，P 点的场强为

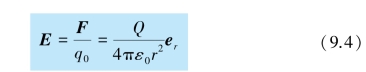
如果以Q 为球心，以r 为半径作一球面，则球面上各点场强的大小相等，方向均沿着球的径向.由此可以看出点电荷场强分布对称的规律性，如图9.6 所示.

4）场强叠加原理

如果电场是由n 个点电荷q1、q2、…、qn所产生，我们可以把这n 个点电荷组成的系统称为点电荷系，如图9.7 所示.若在该电场中任一点处放入一试验电荷q0，则根据力的叠加原理可得，q0 所受的电场力应等于各个点电荷各自对q0 作用的电场力F1、F2、…、Fn的矢量和，即

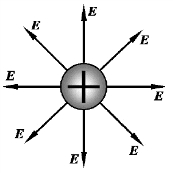
图9.6　点电荷的电场分布

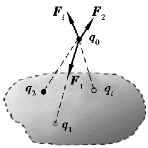
图9.7　电场强度叠加原理

两边同时除以q0，可得

根据场强定义，等式左边是总场强，右边各项分别是各个点电荷单独存在时所产生的场强，由上式可得：在点电荷系的电场中任一点的总场强等于各个点电荷单独存在时在该点产生的场强的矢量和，即

此即电场强度的叠加原理，简称场强叠加原理.

如果带电体上的电荷分布是连续的，则可将其看成许多极小的电荷元dq 的集合.dq 在考察点处的场强可根据点电荷场强公式求得

式中，r 是从电荷元dq 到电场中考察点的距离，er 是dq 指向考察点的单位矢量.根据叠加原理，把所有电荷元对考察点的电场强度求和，数学上对上式求矢量积分，得到电荷系在考察点的电场强度E 为

对于电荷连续分布的带电体，我们可以根据其元电荷分布情况（线分布、面分布或体分布），引入其电荷线密度λ、面密度σ 或体密度ρ，电荷元dq 可分别表示为

则电荷连续分布的三种情况下的带电体的场强分别为

实际上，在具体运算时，有时也先分别写出dE 在x、y、z 三个坐标轴方向上的分量式，然后进行积分计算，最后再合成求出E矢量.

例9.2　相距为l 的一对等量异号点电荷系统称为电偶极子.由负电荷指向正电荷的矢量（矢径）作为电偶极子的轴线的正方向，电量q 与矢径l 的乘积定义为电偶极矩，简称电矩.电矩是矢量，用p 表示，p ＝ql.试求真空中电偶极子的在轴线正方向上和轴线中垂线上的场强.

解　（1）轴线延长线上P 点的场强

如图9.8（a）所示，以l 的中点为原点O 建立坐标系，设点电荷＋q 和－q 轴线的中点O 到轴线延长线上一点P 点的距离为r（r≫l），＋q 和－q 在P 点产生的场强大小分别为

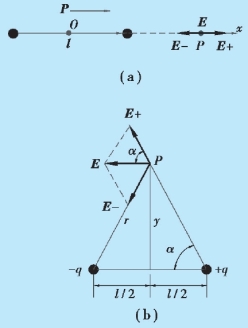
图9.8　例9.2 用图

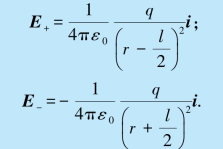
其中i 为沿Ox 轴正向的单位矢量，求E＋和E－的矢量和，因此P 点的合场强EP的大小为

因为r ≫l，所以

写成矢量式为(www.xing528.com)

EP的方向与电矩P 的方向一致.（2）中垂线上P 点的场强

如图9.8（b）所示，设点电荷＋q 和－q 轴线的中点到中垂线上一点P 点的距离为y（y≫l）， ＋q 和－q 在P 点产生的场强大小为

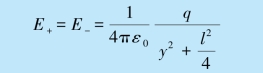
合场强的大小为

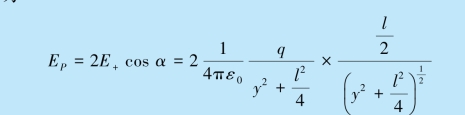
所以，合场强的大小为

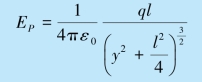
由于y≫l，所以

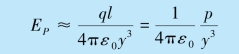
因为EP的方向与电矩的方向相反，写成矢量式为

从上面的计算可知， 电偶极子的场强与q 和l 的乘积成正比，这一乘积反映电偶极子的基本性质，它是一个描述电偶极子属性的物理量.电偶极子是一个重要的物理模型，在研究电磁波的发射和吸收、电介质的极化以及中性分子之间的相互作用等问题时，都要用到这一模型.

例9.3　在真空中有一均匀带电的细棒，电荷线密度为λ，棒外一点P 和棒两端的连线与棒之间的夹角分别为θ1 和θ2，P 点到棒的距离为x，如图9.9（a）所示，求P 点的电场强度.

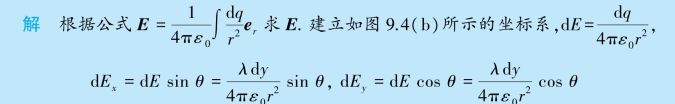
为了把两式中的变量θ、r、y 用单一变量θ 代替，必须进行变量代换.利用几何和三角知识知

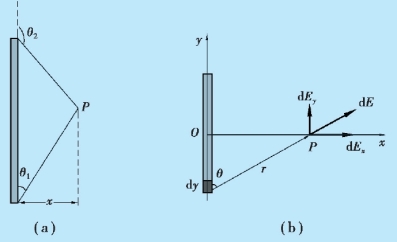
图9.9　例9.3 用图

将以上各式进行整理后得

积分遍及整个带电细棒，θ 从θ1→θ2，于是得

其矢量表达式为

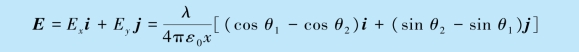
场强的大小为

场强的方向可用E 与x 轴的夹角β 表示

讨论：

例9.4　如图9.10 所示，一半径为R 的均匀带电圆环，电荷总量为q.求轴线上离环中心O 为x 处的场强E.

解　圆环上任一电荷元dq 在P 点产生的场强为

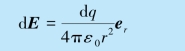
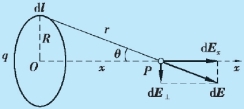
图9.10　例9.4 用图

根据对称性分析，整个圆环在距圆心x 处P 点产生的场强，方向沿x 轴，大小为

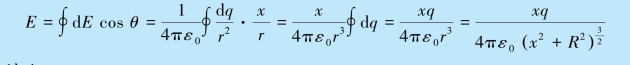
讨论：

（1）若x ＝0，则E＝0.表明环心处的电场强度为零.

例9.5　求均匀带电薄圆盘轴线上的电场强度.设盘的半径为R0，电荷面密度为σ.

解　如图9.11 所示，在圆盘轴线上任取一点P，P点到盘心的距离为x.为了计算圆盘产生的电场强度，把圆盘分成许多同心的细圆环带，取一半径为R，宽度为dR 的细圆环带，其面积为dS ＝2πRdR，所带的电荷量为dq ＝σdS ＝σ2πRdR.由例9.4 可知，此圆环带在P 点产生的电场强度为方向为：当σ＞0 时，沿x 轴正向；当σ＜0 时，沿x 轴负向.由于所有细圆环带在P 点处产生的电场强度的方向都相同，由上式可得带电薄圆盘在轴线上P 点产生的电场强度为

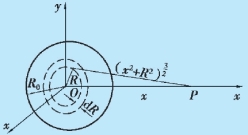
图9.11　例9.5 用图

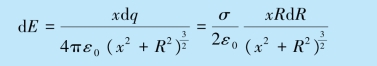
这表明，无限大均匀带电平面所产生的电场强度与场点到平面的距离无关，即在平面两侧各点电场强度大小相等、方向相同且与带电面垂直，平面两侧的电场关于带电平面对称，电场的这种分布称为面对称分布.