无限长圆柱体及半无限长柱面的压力分析

设圆柱的表面r=a受到了如此的压强而变形:当z＞0时表面压强等于f(z),当z＜0时表面压强等于零。对于柱体的整个长度而言,假设表面上的切应力都等于零

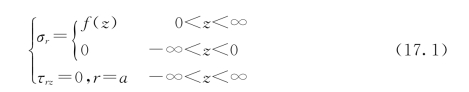
重列满足平衡方程的式(8.3)

应力函数φ满足如下方程

而边界条件成为

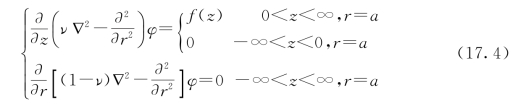
为了用傅里叶变换求解出双调和方程(17.3),将它两边乘以eiξz而对z由-∞到∞求积分,此时假设z的虚数部分是正的。这样,令

而用部分积分法,便可以推知,方程(17.3)是与

等价的,其中

同样,用F(ξ)代表积分

则方程式(17.4)第一式可以写成

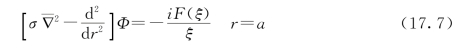
而方程式(17.4)第二式可以写成

方程式(17.6)的解,当r=0时保持有限,是

利用贝塞尔函数的标准循环公式可得

将这个关系式代入边界条件式(17.7),便得到下列方程

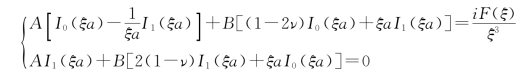
用以决定常数A,B。解出这组方程,即得

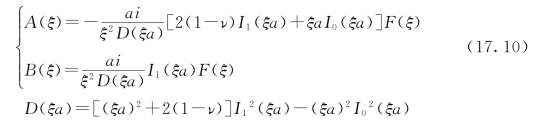
当辅助函数Φ已经决定了以后,应力分量便易于计算。例如,如果将方程式(17.2)第一式两边乘以eiξz而对z由-∞到∞求积分,那么便得到

利用方程式(17.8)与式(17.10)将此式中的Φ表出,则得径向应力σr的变换式∑r

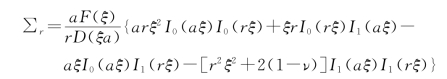
由傅里叶定理

设F(α)为函数f(x)的傅里叶变换式,即(www.xing528.com)

那么f(x)便可以由F(α)用下面的关系式表示

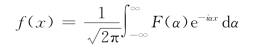
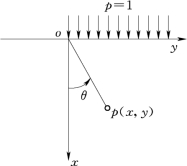
图17.1　一个特别的分布函数

即可由傅里叶变换式∑r而得到应力σr

为确定上面∑r积分中的边界条件函数F(ξ),看图17.1所示的函数

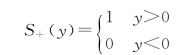
先考虑δ函数

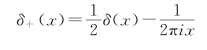
的傅里叶变换

变换式右边正是S+(y),按傅里叶定理反演便得

如令式(17.1)中f(z)=1,则由上可知

将F(ξ)的这种值代入∑r,并将ξ用η=ξa代替,则得

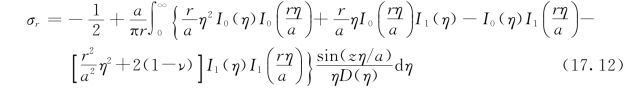
到此,将方程式(17.2)中第2、第3、第4式乘以eiξz而对z由-∞到∞求积分,即可推知,其余应力分量的变换式为

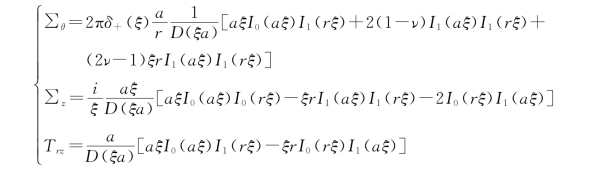
再利用傅里叶定理将这些方程反演,便得到应力分量如下

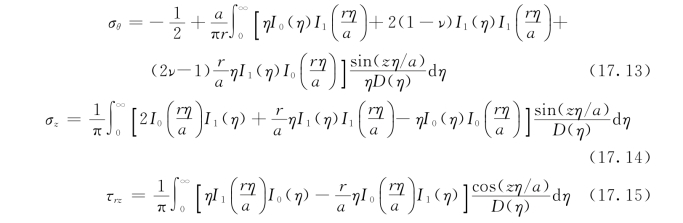
位移也可用如上方法求得,但这里由变形分量式及胡克定律

用已求得的应力来得到径向位移

特别要注意的是,这些结果是在f(z)=1,即1个单位的常量力作用下得到的。当作用力为常量p时,则要将以上结果用p倍乘。或者在表达边界条件的δ(x)式中两边乘以p,后续的演算中因其是常量不会改变,也会是这个结果。

不同r与z的应力σr数值计算结果见图17.2,r=a的柱面径向位移见图17.3。由图17.2中可见,不同r的σr,约在z＜-a/2后有微小的拉应力,约在-a/2＜z＜0的压应力外小内大,约在0＜z＜a/2的压应力外大内小,在z≥a后趋同于施加值。由图17.3可见,ur在z≥-a/2为压缩,约在z＞+a/2后起趋于常量,在a/2～-a/2区间急速下降;在z=-a/2时开始膨胀,z=-2a时趋于零。

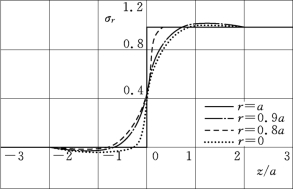
图17.2　径向力σr随r,z的变化

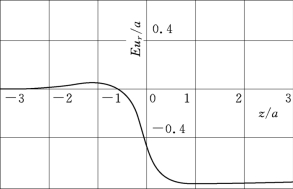
图17.3　柱面径向位移的形态