考察长圆柱体在表面的环带ABCD上受均匀压力p(图16.1)。所需的解答显然可将图16.1所示两种压力分布的影响叠加而得到。因此,基本问题是圆柱面的下半部受压力p/2而上半部受压力-p/2的问题。假定圆柱为无限长,现在来求出这问题的解答。
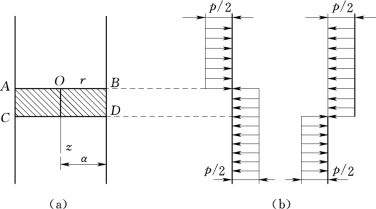
图16.1 两对半无限长柱面反向力叠加成局段同向力
从方程式(15.15)的应力函数开始。将J0(ikr)写作I0(kr),J1(ikr)写作iI1(kr),并令b0=ρb1,于是
不论给k以任何值,这函数都能满足方程(8.4)。如果假定k值有一个变程,就可以认为b1与k和增量dk有关,而写为
代入式(16.1)。并将所有这样的应力函数总加起来,就得到以下形式的更一般的应力函数
现在来考查,怎样才可能选取函数f(k)使得这应力函数给出目前问题的解答。
由式(8.3)求得剪应力是
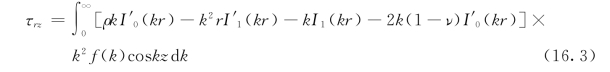
其中上角一撇表示对kr的导数。这应力在r=a得表面上必须成为零。将r=a代入方括号内的表达式,并使它等于零,就得到关于ρ的一个方程,解得
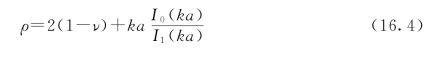(www.xing528.com)
剩下的边界条件是
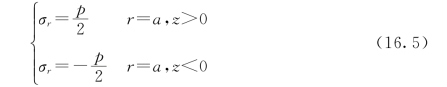
用方程式(8.3),由式(16.2)求得σr的值是
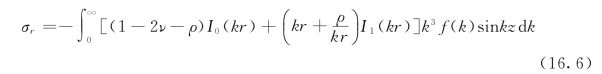
现在利用已知关系
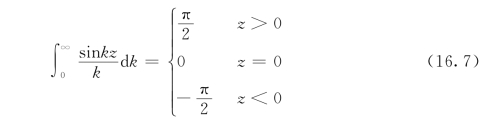
乘以
,得
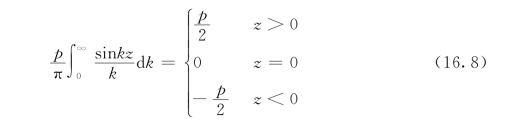
其中右边的值相应于式(16.5)所给出的σr的边界值。因此,如果使方程式(16.6)的右边在r=a时与方程式(16.8)的左边相等,就能满足边界条件式(16.5)。这就要求
由这方程可以确定f(k)。然后就可以用公式(8.3)由应力函数式(16.2)求得各应力分量。这些应力分量将是一些积分式,与σr的表达式(16.6)中的积分具有相同的一般性质。图16.2中的各曲线表明在不同径向距离处的各个应力沿轴向的变化,也表明了表面的位移。根据这些曲线,用本节开始时所说的叠加法,可以求得图16.1所示的问题的结果。当压力带的宽度等于圆柱体的半径时,在压力带中央的表面处,切向应力σθ的值比所施加的压力约大出10%(当然是压应力)。在紧靠压力带外边的表面处,轴向应力σz是拉应力,其值均为施加的压力的45%。在压力带的边缘AB和CD(图16.1)并紧靠表面处,剪应力τrz达到最大值,等于施加的压力的31.8%。
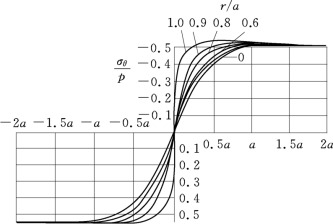
图16.2 环向力σθ随r,z的变化
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
